题目内容
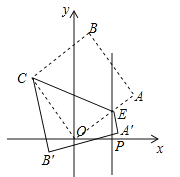
【题目】如图，在平面直角坐标系中，坐标原点O是正方形OABC的一个顶点，已知点B坐标为（1，7），过点P（a，0）（a＞0）作PE⊥x轴，与边OA交于点E（异于点O、A），将四边形ABCE沿CE翻折，点A′、B′分别是点A、B的对应点，若点A′恰好落在直线PE上，则a的值等于（ ）
A．
B．
C．2 D．3
【答案】C．
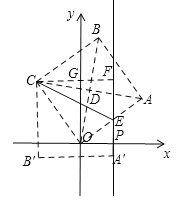
【解析】当点A′恰好落在直线PE上，如图所示，连接OB、AC，交于点D，过点C作CF∥A′B′，交PE于点F，交y轴于点G，则CF⊥y轴，∵四边形OABC是正方形，∴OD=BD，OB⊥AC，∵O（0，0），B（1，7），∴D（
，
），由勾股定理得：OB=
=
=
，设直线OB的解析式为：y=kx，把B（1，7）代入得：k=7，∴直线OB的解析式为：y=7x，∴设直线AC的解析式为：
，把D（，）代入得：
，c=
，∴直线AC的解析式为：
，设C（x，
），在Rt△OBC中，cos∠BOC=
，∴OC=cos45°OB=
=5，∴正方形OABC的边长为5，由翻折得：A′B′=AB=5，在Rt△OCG中，
，∴
，解得：x1=﹣3，x2=4（舍），∴CG=3，∵CF=A′B′=5，∴FG=CF﹣CG=5﹣3=2，∴P（2，0），即a=2，故选C．
练习册系列答案
相关题目
