题目内容
【题目】数学思考: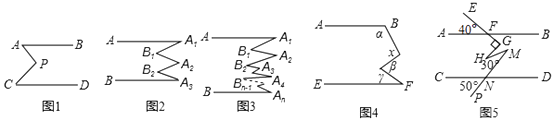
(1)如图1,已知AB∥CD,探究下面图形中∠APC和∠PAB、∠PCD的关系,并证明你的结论
(2)①如图2,已知AA1∥BA1 , 请你猜想∠A1 , ∠B1 , ∠B2 , ∠A2、∠A3的关系,并证明你的猜想;
②如图3,已知AA1∥BAn , 直接写出∠A1 , ∠B1 , ∠B2 , ∠A2、…∠Bn﹣1、∠An的关系
(3)①如图4所示,若AB∥EF,用含α,β,γ的式子表示x,应为
A.180°+α+β﹣γ B.180°﹣α﹣γ+β C.β+γ﹣α D.α+β+γ
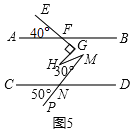
②如图5,AB∥CD,且∠AFE=40°,∠FGH=90°,∠HMN=30°,∠CNP=50°,请你根据上述结论直接写出∠GHM的度数是 .
【答案】
(1)证明:如图1,过点P作OP∥AB,
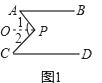
∵AB∥CD,
∴OP∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∴∠APC=∠1+∠2=∠PAB+∠PCD,
即∠APC=∠PAB+∠PCD
(2)解:①如图2,过点A2作A2O∥AA1,
由(1)可知∠B1=∠A1+∠1,∠B2=∠2+∠A3,
所以,∠B1+∠B2=∠A1+∠A2+∠A3;
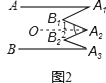
②如图3,由①可知:
∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn﹣1
(3)B,30°
【解析】解:(1)如图1,过点P作OP∥AB,
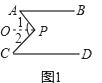
∵AB∥CD,
∴OP∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∴∠APC=∠1+∠2=∠PAB+∠PCD,
即∠APC=∠PAB+∠PCD
(2)①如图2,过点A2作A2O∥AA1,
由(1)可知∠B1=∠A1+∠1,∠B2=∠2+∠A3,
所以,∠B1+∠B2=∠A1+∠A2+∠A3;

②如图3,由①可知:
∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn﹣1
(3)①如图4,过∠x的顶点作CD∥AB,
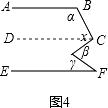
则∠x=(180°﹣α)+(β﹣γ)=180°﹣α﹣γ+β,
②如图5,由(1)可知,40°+∠GHM+50°=∠G+∠M,
∵∠G=90°,∠M=30°,
∴∠GHM=90°+30°﹣40°﹣50°=30°.
所以答案是:(1)∠APC=∠PAB+∠PCD;(2)∠B1+∠B2=∠A1+∠A2+∠A3;∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn﹣1;(3)B;30°.
【考点精析】通过灵活运用平行线的性质,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补即可以解答此题.

 阅读快车系列答案
阅读快车系列答案