题目内容
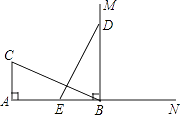
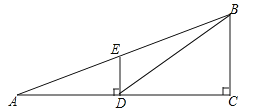
【题目】如图，观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上，从点A处测得楼顶端B的仰角为22°，此时点E恰好在AB上，从点D处测得楼顶端B的仰角为38.5°．已知旗杆DE的高度为12米，试求楼房CB的高度．（参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40，sin38.5°≈0.62，cos38.5°≈0.78，tan38.5°≈0.80）
【答案】24．
【解析】
试题分析：由ED⊥AC，BC⊥AC，得到ED∥BC，得到△AED∽△ABC，由相似得比例，在Rt△AED中，利用锐角三角函数定义求出AD的长，在Rt△BDC中，利用锐角三角函数定义求出BC的长即可．
试题解析：∵ED⊥AC，BC⊥AC，∴ED∥BC，∴△AED∽△ABC，∴
，在Rt△AED中，DE=12米，∠A=22°，∴tan22°=
，即AD=
=30米，在Rt△BDC中，tan∠BDC=
，即tan38.5°==0.8①，∵tan22°=
=0.4②，联立①②得：BC=24米．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
【题目】商场销售A、B两种商品，它们的进价和售价如表所示．
A商品 | B商品 | |
进价（元/件） | 30 | 40 |
售价（元/件） | 50 | 70 |
（1）若该商场购进A、B两种商品共60件，恰好用去2050元，求购进A、B两种商品各多少件？
（2）该商场第二次购买A、B两种商品，而B商品数量比A商品数量的2倍少6件，且购买总额不超过2840元，总利润不少于1900元．请你帮助该商场设计相应的进货方案；
（3）若一个星期该商场销售A、B两种商品的总利润恰好是140元，求销售A、B两种商品各多少件？
