题目内容
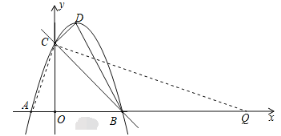
【题目】如图,以![]() 为顶点的抛物线
为顶点的抛物线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,交
,交![]() 轴于点
轴于点![]() .
.
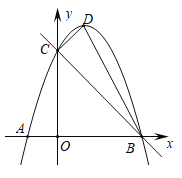
(1)求抛物线的解析式;
(2)在直线![]() 上有一点
上有一点![]() ,使
,使![]() 的值最小,求点
的值最小,求点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)存在,当
;(3)存在,当![]() 的坐标为
的坐标为![]() 或
或![]() 时,以
时,以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
【解析】
(1)将点B和点C的坐标代入二次函数解析式中即可求出结论;
(2)先求出点A的坐标,利用待定系数法求出BC的解析式,作点O关于BC的对称点O′,连接AO′交BC于点P,连接OP,O′B,根据两点之间线段最短,此时![]() 最小,求出点O′的坐标,利用待定系数法求出AO′的解析式,联立方程即可求出结论;
最小,求出点O′的坐标,利用待定系数法求出AO′的解析式,联立方程即可求出结论;
(3)求出顶点D的坐标,利用平面直角坐标系中任意两点之间的距离公式求出CD、BC、CD和AC,根据勾股定理的逆定理证出△BCD是直角三角形,然后根据相似三角形的对应情况分类讨论,根据相似三角形的性质列出比例式即可求出结论.
解:(1)将点B和点C的坐标代入![]() 中,得
中,得
![]()
解得: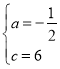
∴抛物线的解析式为![]() ;
;
(2)把y=0代入![]() 中,得
中,得
![]()
解得:x1=-2,x2=6,
∴点A的坐标为(-2,0)
设直线BC的解析式为y=kx+b
将点B和点C的坐标代入,得
![]()
解得:![]()
∴直线BC的解析式为![]()
作点O关于BC的对称点O′,连接AO′交BC于点P,连接OP,O′B
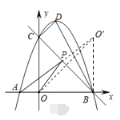
根据对称可得PO=PO′,OB=O′B
此时![]() =
=![]() =
=![]()
根据两点之间线段最短,此时![]() 最小
最小
∵OB=OC=6,∠BOC=90°
∴∠OBC=45°
∴∠OBO′=90°
∵OB= O′B =6
∴点O′的坐标为(6,6)
设直线AO′的解析式为y=mx+n
将点A和点O′的坐标代入,得
![]()
解得: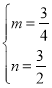
∴直线AO′的解析式为![]()
联立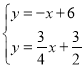
解得: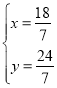
∴点P的坐标为![]()
(3)∵![]() =
=![]()
∴点D的坐标为(2,8)
∴![]()
![]()
∴CD2+BC2=80=BD2
∴△BCD为直角三角形,且∠BCD=90°
点Q在点A左侧时,△QAC为钝角三角形,
∴△QAC不可能与△BCD相似
∴点Q必在点A右侧,设点Q的坐标为(q,0),则AQ=q-(-2)=q+2
∵tan∠CAO=![]() ,tan∠BDC=
,tan∠BDC=![]()
∴∠CAO=∠BDC
当△CQA∽△BCD时,
∴![]()
即![]()
解得:q=0
∴点Q的坐标为(0,0);
当△QCA∽△BCD时,
∴![]()
即![]()
解得:q=18
∴点Q的坐标为(18,0);
综上:点Q的坐标为![]() 或
或![]() .
.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案【题目】在一次数学测验中,八年级(1)班的成绩如下表:
分数 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
人数 | 2 | 3 | 10 | 6 | 4 | 7 | 6 | 2 |
(1)本次数学测验成绩的平均数,中位数,众数各是多少?
(2)若老师把人数中的数据“10”看成了“9”,数据“7”看成了“8”,则平均数,中位数,众数中不受影响的是________.