题目内容
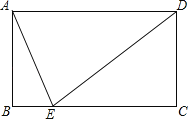
【题目】如图，已知Rt△EBC中，∠B＝90°，A为BE边上一点，以边AC上的点O为圆心、OA为半径的圆O与EC相切，D为切点，AD∥BC．
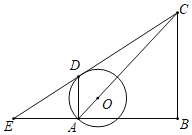
（1）求证：∠E＝∠ACB．
（2）若AD＝1，
，求BC的长．
【答案】（1）见解析；（2）2
【解析】
（1）连结OD，通过切线的性质可知OD⊥EC，再由同角的余角相等即可得到∠E＝∠ODA，再根据等腰三角形的性质及平行线的性质即可得到∠E＝∠ACB；
（2）设AB＝x，通过相同锐角的三角函数值相同，即可得到
，再根据
得到
进行求解即可得解.
（1）连结OD
∵AD∥BC，
∴
∴
又圆O与EC相切于D点
∴OD⊥EC
∴
∴∠E＝∠ODA
又OD＝OA
∴∠DAC＝∠ODA
∴∠DAC＝∠E
∵AD∥BC
∴∠DAC＝∠ACB
∴∠E＝∠ACB；
（2）由（1）知，∠E＝∠ACB＝∠DAC，
∴
∴在
中，
∵AD＝1
∴
设AB＝x
∵在
中，
∴
∵AD∥BC
∴
∴
∴
∴
经检验是所列方程的根，
∴
．
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案【题目】某学校在A、B两个校区各有九年级学生200人，为了解这两个校区九年级学生的教学学业水平的情况，进行了抽样调查，过程如下，请补充完整．
收集数据：从A、B两个校区各随机抽取20名学生，进行了数学学业水平测试，测试成绩（百分制）如下：
A校区 86 74 78 81 76 75 86 70 75 90
75 79 81 70 74 80 87 69 83 77
B校区 80 73 70 82 71 82 83 93 77 80
81 93 81 73 88 79 81 70 40 83
整理、描述数据 按如下分数段整理、描述这两组样本数据：
成绩x 人数 校区 | 40≤x＜50 | 50≤x＜60 | 60≤x＜70 | 70≤x＜80 | 80≤x＜90 | 90≤x≤100 |
A | 0 | 0 | 1 | 11 | 7 | 1 |
B |
（说明：成绩80分及以上的学业水平优秀，70﹣79分为淡定业水平良好，60﹣69分为学业水平合格，60分以下为学业水平不合格）
分析数据 两组样本数据的平均数、中位数、众数如下表所示：
校区 | 平均数 | 中位数 | 众数 |
A | 78.3 | m | 75 |
B | 78 | 80.5 | 81 |
其中m＝ ；
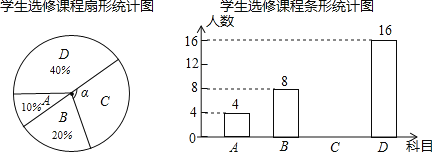
得出结论：a．估计B校区九年级数学学业水平在优秀以上的学生人数为 ；
b．可以推断出 校区的九年级学生的数学学业水平较高，理由为 （至少从两个不同的角度说明推断的合理性）．
【题目】某校开展主题为“垃圾分类，绿色生活新时尚”的宣传活动，为了解学生对垃圾分类知识的掌握情况，学生会随机抽取了20名七、八年级学生（每个年级各10人）进行问卷调查，并把他们的得分绘制成了如下表格，计分采用10分制（得分均取整数）成绩达到6分或6分以上为及格，达到9分及以上为优秀，成绩如表1所示，并制作了成绩分析表（表2）．
表1
七年级 | 5 | 8 | 8 |
| 8 | 10 | 10 | 8 | 5 | 5 |
八年级 | 10 | 6 | 6 | 9 |
| 4 | 5 | 7 | 10 | 8 |
表2
年级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
七年级 | 7.6 | 8 | 8 | 3.82 | 70% |
|
八年级 | 7.5 |
| 10 | 4.94 | 80% | 40% |
（1）在表1中，
_____，
_____；在表2中，
_____，
______；
（2）根据表2成绩数据分析，你认为哪个年级的学生对垃圾分类了解更加深入，请说明你的理由；
（3）小明根据表2数据作出如下判断：
①七年级学生成绩的平均数高于八年级，故七年级学生一定比八年级学生优秀；
②被调查对象中，七年级学生的成绩更加稳定；
③学校七年级和八年级共有400人，估计有280人成绩达到优秀；
④七年级不及格人数比八年级多；
对小明的四个结论，随机任选两个，求都是错误的概率．
