题目内容
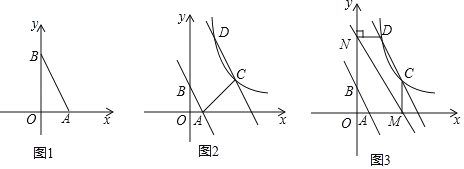
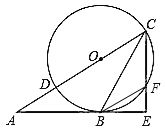
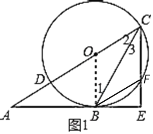
【题目】如图,已知Rt△ACE中,∠AEC=90°,CB平分∠ACE交AE于点B,AC边上一点O,⊙O经过点B、C,与AC交于点D,与CE交于点F,连结BF。
(1)求证:AE是⊙O的切线;
(2)若![]() ,AE=8,求⊙O的半径;
,AE=8,求⊙O的半径;
(3)在(2)条件下,求BF的长。
【答案】(1)证明见解析 (2)![]() (3)
(3)![]()
【解析】
(1) 连接OB,根据OB=OC得出∠1=∠2,再根据CB平分∠ACE,得出∠2=∠3,再利用平行线的性质求解即可;(2) 连接DF,根据同弧所对圆周角相等得出∠CDF=∠CBF,再利用直径所对的圆周角为90°,得出∠DFC=90°,由OB//CE,得出△AOB∽△ACE,利用相似三角形的性质,列出方程求解即可;(3) 先证出△ACB∽△BCF,再利用相似三角形的性质得出![]() =
=![]() ,进而求出结果.
,进而求出结果.
(1)证明:如图1,连接OB,
∵OB=OC,∴∠1=∠2,
∵CB平分∠ACE,∴∠2=∠3,
∴∠1=∠3,∴OB∥CE,
∴∠ABO=∠AEC=90°,即OB丄AE,
∴AE是⊙0的切线;
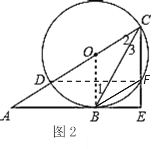
(2)如图2,连接DF,
∵∠CDF和∠CBF是同弧所对圆周角,
∴∠CDF=∠CBF,
∵CD是⊙O的直径,∴∠DFC=90°,
∴DF//AE,∴∠A=∠CDF,∴∠A=∠CBF,
∵cos∠CBF=![]() ,∴cosA=
,∴cosA=![]() ,
,
在Rt△ACE中AE=8,∴AC=10,CE=6,
由(1)可知OB//CE,∴△AOB∽△ACE,
∴![]() ,
,
设⊙O的半径为x,则![]() ,
,
解得x=![]() ,∴⊙O的半径为
,∴⊙O的半径为![]() ;
;
(3)在Rt△AOB中AO=10-![]() =
=![]() ,cos A=
,cos A=![]() ,∴AB=5,
,∴AB=5,
在Rt△DCF中CD=![]() ,cos∠CDF=cos∠CBF=
,cos∠CDF=cos∠CBF=![]() ,∴CF=
,∴CF=![]() ,
,
∵∠A=∠CBF,∠2=∠3,
∴△ACB∽△BCF,
∴![]() =
=![]() ,
,
∴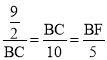 ,
,
解得,BC=![]() ,BF=
,BF=![]() .
.

练习册系列答案
相关题目