题目内容
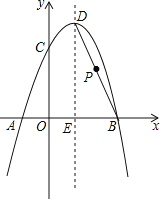
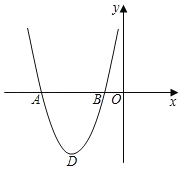
【题目】如图,在平面直角坐标系中,抛物线C1经过点A(﹣4,0)、B(﹣1,0),其顶点为![]() .
.
(1)求抛物线C1的表达式;
(2)将抛物线C1绕点B旋转180°,得到抛物线C2,求抛物线C2的表达式;
(3)再将抛物线C2沿x轴向右平移得到抛物线C3,设抛物线C3与x轴分别交于点E、F(E在F左侧),顶点为G,连接AG、DF、AD、GF,若四边形ADFG为矩形,求点E的坐标.
【答案】(1)y![]() ;(2)
;(2)![]() ;(3)E(
;(3)E(![]() ,0).
,0).
【解析】
(1)根据抛物线C1的顶点坐标可设顶点式将点B坐标代入求解即可;
(2)由抛物线C1绕点B旋转180°得到抛物线C2知抛物线C2的顶点坐标,可设抛物线C2的顶点式,根据旋转后抛物线C2开口朝下,且形状不变即可确定其表达式;
(3)作GK⊥x轴于G,DH⊥AB于H,由题意GK=DH=3,AH=HB=EK=KF![]() ,结合矩形的性质利用两组对应角分别相等的两个三角形相似可证△AGK∽△GFK,由其对应线段成比例的性质可知AK长,结合A、B点坐标可知BK、BE、OE长,可得点E坐标.
,结合矩形的性质利用两组对应角分别相等的两个三角形相似可证△AGK∽△GFK,由其对应线段成比例的性质可知AK长,结合A、B点坐标可知BK、BE、OE长,可得点E坐标.
解:(1)∵抛物线C1的顶点为![]() ,
,
∴可设抛物线C1的表达式为y![]() ,
,
将B(﹣1,0)代入抛物线解析式得:![]() ,
,
∴![]() ,
,
解得:a![]() ,
,
∴抛物线C1的表达式为y![]() ,即y
,即y![]() .
.
(2)设抛物线C2的顶点坐标为![]()
∵抛物线C1绕点B旋转180°,得到抛物线C2,即点![]() 与点
与点![]() 关于点B(﹣1,0)对称
关于点B(﹣1,0)对称
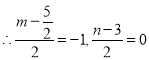
![]()
∴抛物线C2的顶点坐标为(![]() )
)
可设抛物线C2的表达式为y![]()
∵抛物线C2开口朝下,且形状不变
![]()
∴抛物线C2的表达式为y![]() ,即
,即![]() .
.
(3)如图,作GK⊥x轴于G,DH⊥AB于H.
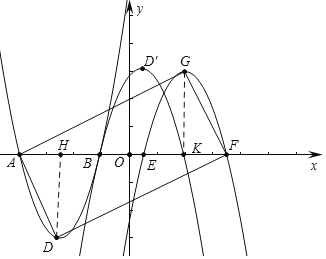
由题意GK=DH=3,AH=HB=EK=KF![]() ,
,
∵四边形AGFD是矩形,
∴∠AGF=∠GKF=90°,
∴∠AGK+∠KGF=90°,∠KGF+∠GFK=90°,
∴∠AGK=∠GFK.
∵∠AKG=∠FKG=90°,
∴△AGK∽△GFK,
∴![]() ,
,
∴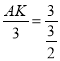 ,
,
∴AK=6,
![]() ,
,
∴BE=BK﹣EK=3![]() ,
,
∴OE![]() ,
,
∴E(![]() ,0).
,0).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
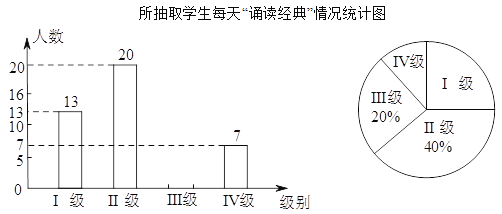
小学生10分钟应用题系列答案【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
满意度 | 人数 | 所占百分比 |
非常满意 | 12 | 10% |
满意 | 54 | m |
比较满意 | n | 40% |
不满意 | 6 | 5% |

根据图表信息,解答下列问题:
(1)本次调查的总人数为______,表中m的值为_______;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.