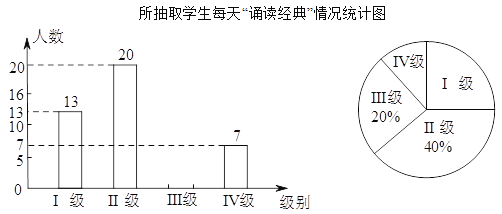
题目内容
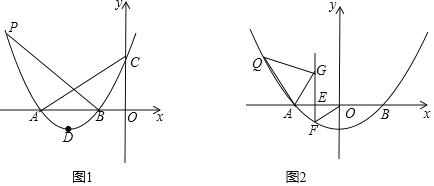
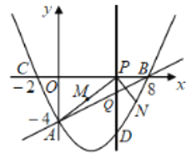
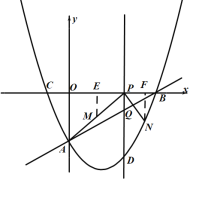
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 过点
过点![]() ,动点P在线段
,动点P在线段![]() 上以每秒2个单位长度的速度由点
上以每秒2个单位长度的速度由点![]() 运动到点
运动到点![]() 停止,设运动时间为
停止,设运动时间为![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() , 交抛物线于点
, 交抛物线于点![]() .连接
.连接![]() ,
,![]() 是线段
是线段![]() 的中点,将线段
的中点,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() .
.
(1)求抛物线的解析式;
(2)连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 面积有最大值,最大值是多少?
面积有最大值,最大值是多少?
(3)当![]() 为何值时,点
为何值时,点![]() 落在抛物线上.
落在抛物线上.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 面积的最大值为16;(3)
面积的最大值为16;(3)![]()
【解析】
(1)用待定系数法即可求出抛物线的解析式;
(2)先用待定系数法求出直线AB的解析式,然后根据点P的坐标表示出Q,D的坐标,进一步表示出QD的长度,从而利用面积公式表示出![]() 的面积,最后利用二次函数的性质求最大值即可;
的面积,最后利用二次函数的性质求最大值即可;
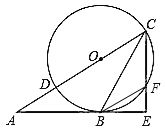
(3)分别过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足分别为
,垂足分别为![]() ,首先证明
,首先证明![]() ≌
≌![]() ,得到
,得到![]() ,然后得到点N的坐标,将点N的坐标代入抛物线的解析式中,即可求出t的值,注意t的取值范围.
,然后得到点N的坐标,将点N的坐标代入抛物线的解析式中,即可求出t的值,注意t的取值范围.
(1)∵抛物线![]() 过点
过点![]() ,
,
∴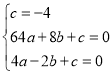 解得
解得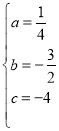
所以抛物线的解析式为:![]() ;
;
(2)设直线AB的解析式为![]() ,
,
将![]() 代入解析式中得,
代入解析式中得,
![]() 解得
解得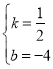
∴直线AB解析式为![]() .
.
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 面积的最大值为16 ;
面积的最大值为16 ;
(3)分别过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足分别为
,垂足分别为![]() ,
,
![]()
![]() .
.
在![]() 和
和![]() 中,
中,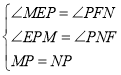 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() .
.
∵![]() ,
,
![]() .
.
当点![]() 落在抛物线上时,
落在抛物线上时,![]() .
.
∴![]() ,
,
![]() ,
,
∴![]() .
.

练习册系列答案
相关题目