题目内容
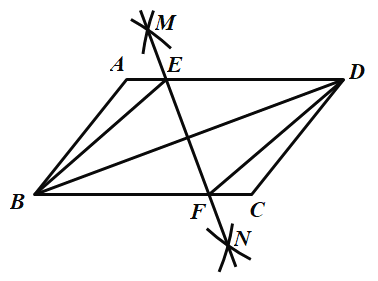
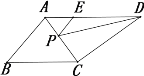
【题目】如图，四边形ABCD中，AD∥BC，AC平分∠BAD，∠ABC=60°，E为AD上一点，AE=2，DE=4，P为AC 上一点，则△PDE周长的最小值为_______．
【答案】
【解析】
作出点E关于AC的对称点，确定△PDE周长最小时P的位置，过F作AD垂线，构造Rt
AFG和RtDFG，即可得出结果．
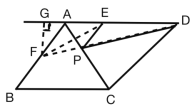
如图，作点E关于AC的对称点F，此时PF=PE，连接FD交AC于点P，
∴△PDE周长为：DE+PE+PD=DE+PF+PD
∵DE=4固定，△PDE周长最小及PF+PD最小，故P，D，F三点共线
∵AC平分∠BAD，∴
∵
，
∴
，即
∵
，
为等边三角形
∴
∴
∵AF=AE=2，
∴AG=1，FG=
，GD=7
∴
△PDE周长为：DE+PE+PD=DE+PF+PD=DE+DF=4+
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
【题目】某超市以20元/kg的价格购进一批商品进行销售，根据以往的销售经验及对市场行情的调研，该超市得到日销售量y（kg）与销售价格x（元/kg）之间的关系，部分数据如下表：
销售价格x（元/kg） | 25 | 30 | 35 | 40 | … |
日销售量y（kg） | 1000 | 800 | 600 | 400 | … |
（1）根据表中的数据，用所学过的函数知识确定y与x之间的函数关系式；
（2）超市应如何确定销售价格，才能使日销售利润W（元）最大？W最大值为多少？
（3）供货商为了促销，决定给予超市a元/kg的补贴，但希望超市在30≤x≤35时，最大利润不超过10240元，求a的最大值．
