题目内容
【题目】如图,抛物线y=a(x﹣1)(x﹣3)与x轴交于A,B两点,与y轴的正半轴交于点C,其顶点为D.
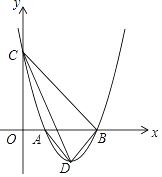
(1)写出C,D两点的坐标(用含a的式子表示);
(2)设S△BCD:S△ABD=k,求k的值;
(3)当△BCD是直角三角形时,求对应抛物线的解析式.
【答案】(1) C(0,3a),D(2,﹣a);(2)3;(3) y=x2﹣4x+3或y= ![]() x2﹣2
x2﹣2![]() x+
x+ ![]() .
.
【解析】(1)令x=0可求得C点坐标,化为顶点式可求得D点坐标;
(2)令y=0可求得A、B的坐标,结合D点坐标可求得△ABD的面积,设直线CD交x轴于点E,由C、D坐标,利用待定系数法可求得直线CD的解析式,则可求得E点坐标,从而可表示出△BCD的面积,可求得k的值;
(3)由B、C、D的坐标,可表示出BC2、BD2和CD2,分∠CBD=90°和∠CDB=90°两种情况,分别利用勾股定理可得到关于a的方程,可求得a的值,则可求得抛物线的解析式.
(1)在y=a(x﹣1)(x﹣3),令x=0可得:y=3a,∴C(0,3a).
∵y=a(x﹣1)(x﹣3)=a(x2﹣4x+3)=a(x﹣2)2﹣a,∴D(2,﹣a);
(2)在y=a(x﹣1)(x﹣3)中,令y=0可解得:x=1或x=3,∴A(1,0),B(3,0),∴AB=3﹣1=2,∴S△ABD=![]() ×2×a=a.
×2×a=a.
如图,设直线CD交x轴于点E,设直线CD解析式为y=tx+b,把C、D的坐标代入可得![]() ,解得:
,解得:![]() ,
,
∴直线CD解析式为y=﹣2ax+3a,令y=0可解得:x=![]() ,∴E(
,∴E(![]() ,0),∴BE=3﹣
,0),∴BE=3﹣![]() =
=![]() ,
,
∴S△BCD=S△BEC+S△BED=![]() ×
×![]() ×(3a+a)=3a,∴S△BCD:S△ABD=(3a):a=3,∴k=3;
×(3a+a)=3a,∴S△BCD:S△ABD=(3a):a=3,∴k=3;
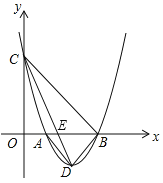
(3)∵B(3,0),C(0,3a),D(2,﹣a),∴BC2=32+(3a)2=9+9a2,CD2=22+(﹣a﹣3a)2=4+16a2,BD2=(3﹣2)2+a2=1+a2.
∵∠BCD<∠BCO<90°,∴△BCD为直角三角形时,只能有∠CBD=90°或∠CDB=90°两种情况.
①当∠CBD=90°时,则有BC2+BD2=CD2,即9+9a2+1+a2=4+16a2,解得:a=﹣1(舍去)或a=1,此时抛物线解析式为y=x2﹣4x+3;
②当∠CDB=90°时,则有CD2+BD2=BC2,即4+16a2+1+a2=9+9a2,解得:a=﹣![]() (舍去)或a=
(舍去)或a=![]() ,此时抛物线解析式为y=
,此时抛物线解析式为y=![]() x2﹣2
x2﹣2![]() x+
x+![]() ;
;
综上可知:当△BCD是直角三角形时,抛物线的解析式为y=x2﹣4x+3或y=![]() x2﹣2
x2﹣2![]() x+
x+![]() .
.