Question

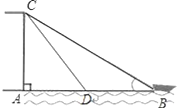
【题目】已知：如图，有人在岸上点C的地方，用绳子拉船靠岸，开始时，绳长CB=10米，CA⊥AB，且CA=6米，拉动绳子将船从点B沿BA方向行驶到点D后，绳长CD=6 米．

（1）试判定△ACD的形状，并说明理由；

（2）求船体移动距离BD的长度．

Answer 1

【答案】（1）△ACD是等腰直角三角形；（2）船体移动距离BD的长度为2m．

【解析】

（1）直接利用勾股定理得出AD的长，进而得出△ACD的形状；

（2）利用勾股定理得出AB的长，进而得出BD的长．

解：（1）由题意可得：AC=6m，DC=6m，∠CAD=90°，

可得AD==6（m），

故△ACD是等腰直角三角形；

（2）∵AC=6m，BC=10m，∠CAD=90°，

∴AB==8（m），

则BD=AB-AD=8-6=2（m）．

答：船体移动距离BD的长度为2m．