Question

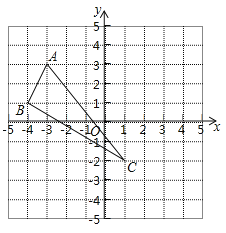
【题目】如图1，在平面直角坐标系中，A（-2，0），B（0，6），C（6，0），∠ABC+∠ADC=180°，BC⊥CD．

(1)求证：∠ABO=∠CAD；

(2)求四边形ABCD的面积；

(3)如图2，E为∠BCO的邻补角的平分线上的一点，且∠BEO=45°，OE交BC于点F，求BF的长．

Answer 1

【答案】(1)证明见解析；(2)32；(3)6.

【解析】

（1）根据四边形的内角和定理、直角三角形的性质证明；
（2）过点A作AF⊥BC于点F，作AE⊥CD的延长线于点E，作DG⊥x轴于点G，证明△ABF≌△ADE、△ABO≌△DAG，利用面积和可得四边形ABCD的面积；
（3）作EH⊥BC于点H，作EG⊥x轴于点G，根据角平分线的性质得到EH=EG，证明△EBH≌△EOG，得到EB=EO，根据等腰三角形的判定定理解出即可．

(1)如图1，在四边形ABCD中，∵∠ABC+∠ADC=180°，

∴∠BAD+∠BCD=180°．

∵BC⊥CD，

∴∠BCD=90°．

∴∠BAD=90°．

∴∠BAC+∠CAD=90°．

又∵∠BAC+∠ABO=90°．

∴∠ABO=∠CAD．

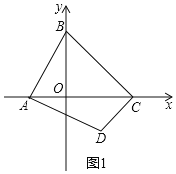
(2)如图2，过点A作AF⊥BC于点F，作AE⊥CD的延长线于点E，作DG⊥x轴于点G．

∵A（-2，0），B（0，6），C（6，0），

∴OA=2，OB=OC=6．

∴∠BCO=45°．

又∵BC⊥CD，

∴∠BCO=∠DCO=45°．

又∵AF⊥BC，AE⊥CD，

∴AF=AE，∠FAE=90°．

∴∠BAF=∠DAE，

∴△ABF≌△ADE．

∴AB=AD．

又∵∠AGD=∠BOA=90°，

∴△ABO≌△DAG．

∴DG=AO=2，AC=AO+OC=8．

∴S四边形ABCD=AC（BO+DG）==32．

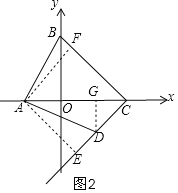
(3)如图3，过点E作EH⊥BC于点H，作EG⊥x轴于点G，

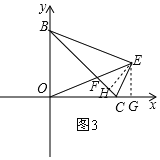
∵E点在∠BCO的邻补角的平分线上，

∴EH=EG．

又∵∠BCO=∠BEO=45°，

∴∠EBC=∠EOC．

∴△EBH≌△EOG．

∴EB=EO．

又∵∠BEO=45°，

∴∠EBO=∠EOB=67.5°．

∵∠OBC=45°，

∴∠BOE=∠BFO=67.5°．

∴BF=BO=6．