题目内容
【题目】如图，
，
均是边长为
的等边三角形，点
是边
、
的中点，直线
、
相交于点
．当绕点旋转时，线段
长的最小值是（ ）
A. 2-
B. +1 C. 
D. -1
【答案】D
【解析】
如图，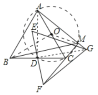
取AC的中点O，连接AD、DG、BO、OM，通过求证△DAG∽△DCF得到∠DAG＝∠DCF;利用四边形的对角互补可得A、D、C、M四点共圆，继而利用三边关系可知BO≤BM＋OM,即BM≥BO－OM;根据两点之间线段最短可得当M在线段BO与该圆的交点处时，线段BM最小，只需求出BO、OM的值，就可解决问题.
如图，取AC的中点O，连接AD、DG、BO、OM，∵△ABC，△EFG均是边长为2的等边三角形，点D是边BC、EF的中点，∴AD⊥BC，GD⊥EF，DA＝DG，DC＝DF，∴∠ADG＝90°－∠CDG＝∠FDC，
，∴△DAG∽△DCF，∴∠DAG＝∠DCF，∴A、D、C、M四点共圆，根据两点之间线段最短可得：BO≤BM＋OM,即BM≥BO－OM，当M在线段BO与该圆的交点处时，线段BM最小，此时，BO＝
＝
，OM＝
AC＝1，则BM＝BO－OM＝－1，故答案选D.
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
