Question

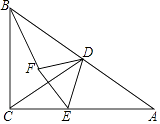
【题目】如图，CD是△ABC的中线，CE是△ABC的高，若AC＝9，BC＝12，AB＝15.

(1)求CD的长．

(2)求DE的长．

Answer 1

【答案】(1)7.5;(2)2.1.

【解析】

（1）利用勾股定理的逆定理得到三角形ABC为直角三角形，再根据直角三角形的性质可求CD的长．
（2）根据三角形的面积公式可求CE，再根据勾股定理可求DE的长．

(1)由AC＝9，AB＝15，BC＝12，

AC2＋BC2＝81+144== AB2

∴∠ACB＝90°，

∵点D是AB的中点，

∴CD＝AB＝7.5；

(2)由∠ACB＝90°，可得S△ABC＝AC·BC＝AB·CE，

∴×9×12＝×15CE，

解得CE＝7.2，

Rt△CDE中，DE＝＝2.1.

故答案为：(1)7.5;(2)2.1.