Question

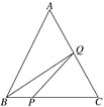
【题目】在△ABC中，已知AB＝BC＝CA＝4 cm，点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1 cm/s；点Q沿CA、AB向终点B运动，速度为2 cm/s，设它们运动的时间为x(s)，当x＝__________，△BPQ是直角三角形．

Answer 1

【答案】2或

【解析】

用t表示出BP、CQ、BQ，然后分两种情况：①∠BPQ=90°，②∠BQP=90°进行讨论即可得解．

分析题意可知，只有点Q运动到AB上时，△BPQ才有可能是直角三角形，根据题意，得B、C两点运动的距离BP＝tcm，CQ＝2tcm， ∴BQ＝(8－2t) cm，

若△BPQ是直角三角形，则∠BPQ＝90°或∠BQP＝90°，

①当∠BPQ＝90°时，

Q在A点，CQ＝CA＝4 cm，

4÷2＝2(s)；

②当∠BQP＝90°时，∵∠B＝60°，

∴∠BPQ＝90°－60°＝30°，

∴BQ＝BP，

即8－2t＝t，

解得t＝，

故当t＝2或秒时，△BPQ是直角三角形．

故答案为：2或 .