题目内容
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°.点D是AB中点,点E为边AC上一点,连接CD,DE,以DE为边在DE的左侧作等边三角形DEF,连接BF.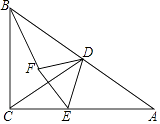
(1)△BCD的形状为;
(2)随着点E位置的变化,∠DBF的度数是否变化?并结合图说明你的理由;
(3)当点F落在边AC上时,若AC=6,请直接写出DE的长.
【答案】
(1)等边三角形
(2)解:∠DBF的度数不变,理由如下:
∵∠ACB=90°,点D是AB中点,
∴CD= ![]() AB=AD,
AB=AD,
∴∠ECD=30°.
∵△BDC为等边三角形,
∴BD=DC,∠BDC=60°.
又∵△DEF为等边三角形,
∴DF=DE,∠FDE=60°,
∴∠BDF+∠FDC=∠EDC+∠FDC=60°,
∴∠BDF=∠CDE.
在△BDF和△CDE中, 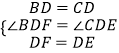 ,
,
∴△BDF≌△CDE(SAS),
∴∠DBF=∠DCE=30°,
即∠DBF的度数不变
(3)解:过点E作EM⊥AB于点M,如图所示.
在Rt△ABC中,∠A=30°,AC=6,
∴AB=2BC,AC= ![]() =
= ![]() BC=6,
BC=6,
∴BC=2 ![]() ,AB=4
,AB=4 ![]() .
.
∵△DEF为等边三角形,
∴∠DEF=60°,
∵∠A=30°,
∴∠ADE=30°,
∴DE=AE,
∴AM= ![]() AD=
AD= ![]() ×
× ![]() AB=
AB= ![]() .
.
在Rt△AME中,∠A=30°,AM= ![]() ,
,
∴AE=2EM,AM= ![]() =
= ![]() EM,
EM,
∴EM=1,AE=2,
∴DE=2.
【解析】解:(1)∵在Rt△ABC中,∠C=90°,∠A=30°,
∴AB=2BC,∠CBD=60°.
∵点D是AB中点,
∴BD=BC,
∴△BCD为等边三角形.
所以答案是:等边三角形.
【考点精析】掌握等边三角形的性质和含30度角的直角三角形是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案