��Ŀ����
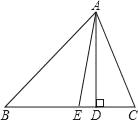
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABCΪ����ֱ�������Σ���ACB=90�㣬������y=��x2+bx+c����A��B���㣬���е�A��C������ֱ�Ϊ��1��0��������4��0���������ߵĶ���Ϊ��D��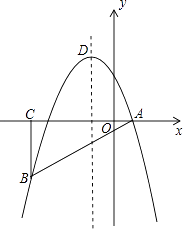
��1���������ߵĽ���ʽ��
��2����E��ֱ��������ABCб��AB�ϵ�һ�����㣨����A��B�غϣ�������E��x��Ĵ��ߣ����������ڵ�F�����߶�FE�ij������ʱ�����E�����ꣻ
��3���ڣ�2���������£����������Ƿ����һ��P��ʹ��PEF����EFΪֱ�DZߵ�ֱ�������Σ������ڣ�������е�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1���⣺��A��C������ֱ�Ϊ��1��0��������4��0����
��AC=5��
�ߡ�ABCΪ����ֱ�������Σ���C=90�㣬
��BC=AC=5��
��B����4����5����
����A�͵�B���������ã� ![]() ����ã�
����ã� ![]() ��
��
�������ߵĽ���ʽΪy=��x2��2x+3��
��2���⣺��ͼ1��ʾ��
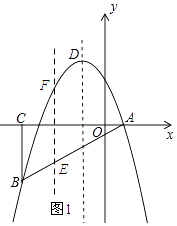
��ֱ��AB�Ľ���ʽΪy=kx+b������A�͵�B���������ã� ![]() ����ã�k=1��b=��1��
����ã�k=1��b=��1��
����ֱ��AB�Ľ���ʽΪy=x��1��
���E��������t��t��1�������F��������t����t2��2t+3����
��EF=��t2��2t+3����t��1��=��t2��3t+4=��t+ ![]() ��2+
��2+ ![]() ��
��
�൱t=�� ![]() ʱ��FEȡ���ֵ
ʱ��FEȡ���ֵ ![]() ����ʱ����E������Ϊ����
����ʱ����E������Ϊ���� ![]() ����
���� ![]() ����
����
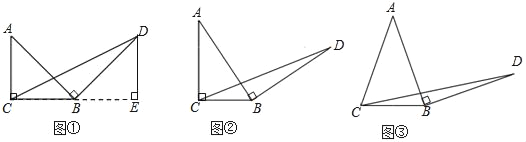
��3���⣺���ڵ�P����ʹ��PEF����EFΪֱ�DZߵ�ֱ�������Σ�
���ɣ���ͼ��ʾ������F��ֱ��a��EF�����������ڵ�P������E��ֱ��b��EF����������P�䡢P�壮
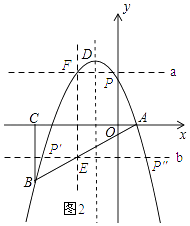
�ɣ�2����֪��E������Ϊ��t��t��1�������F������Ϊ��t����t2��2t+3����t=�� ![]() ��
��
���E���� ![]() ����
���� ![]() ����F����
����F���� ![]() ��
�� ![]() ����
����
�ٵ���t2��2t+3= ![]() ʱ����ã�x=��
ʱ����ã�x=�� ![]() ��x=��
��x=�� ![]() ����ȥ����
����ȥ����
���P���������� ![]() ��
�� ![]() ����
����
�ڵ���t2��2t+3=�� ![]() ʱ����ã�x=��1+
ʱ����ã�x=��1+ ![]() ��x=��1��
��x=��1�� ![]() ��
��
���P�䣨��1�� ![]() ����
���� ![]() ����P�壨��1+
����P�壨��1+ ![]() ����
���� ![]() ����
����
������������P���������� ![]() ��
�� ![]() ����1��
����1�� ![]() ����
���� ![]() ����P�壨��1+
����P�壨��1+ ![]() ����
���� ![]() ����
����
����������1��Ҫ�����ʽ�ؼ�������B�����꣬�ɡ�ABCΪ����ֱ�������Σ���C=90�㣬BC=AC=5�������B����4����5������A��B����������ʽ���ɣ���2������ֵ����ɻ���Ϊ������ֵ���⣬����빹����E�������tΪ�Ա�����EF����Ϊ������ĺ�������t�Ĵ���ʽ��ʾEF��EF����ֱ�߶Σ��䳤�ȿ����϶˵���������¶˵������꣬�������������Ƕ��κ��������䷽�������ֵ����3����EFΪֱ�DZߵ�ֱ�������οɷ�Ϊ���ࣺ��EΪֱ�Ƕ��㣻��FΪֱ�Ƕ��㣻������E��F�ֱ���EF�Ĵ��� �������ߵĽ������P��.