题目内容
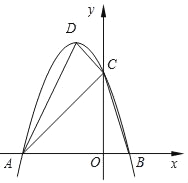
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与x轴交于点A和点B(1,0),与y轴相交于点C(0,3).
(1)求抛物线的解析式和顶点D的坐标;
(2)求证:∠DAB=∠ACB;
(3)点Q在抛物线上,且△ADQ是以AD为底的等腰三角形,求Q点的坐标.
【答案】(1)(﹣1,4);(2)∠DAB=∠ACB;(3)![]() ,
,![]()
【解析】试题分析:(1)把B、C坐标代入抛物线解析式中,解方程组即可得到抛物线解析式,从而得到抛物线顶点坐标;
(2)由tan∠OCB=![]() .tan∠DAC=
.tan∠DAC=![]() ,得到∠DAC=∠OCB,从而得到结论;
,得到∠DAC=∠OCB,从而得到结论;
(3)令Q(x,y)且满足![]() ,由△ADQ是以AD为底的等腰三角形,得到QD2=QA2,从而得到x-2+2y=0.解方程组
,由△ADQ是以AD为底的等腰三角形,得到QD2=QA2,从而得到x-2+2y=0.解方程组![]() ,即可得到结论.
,即可得到结论.
试题解析:解:(1)把B(1,0)和C(0,3)代入![]() 中,
中,
得:![]() ,解得:
,解得:![]() .
.
∴抛物线的解析式是:![]() ,∴顶点坐标D(-1,4).
,∴顶点坐标D(-1,4).
(2)令y=0,则![]() ,x1=-3,x2=1,∴A(-3,0),∴OA=OC=3,∴∠CAO=∠OCA.在Rt△BOC中,tan∠OCB=
,x1=-3,x2=1,∴A(-3,0),∴OA=OC=3,∴∠CAO=∠OCA.在Rt△BOC中,tan∠OCB=![]() .
.
∵AC=![]() ,DC=
,DC=![]() ,AD=
,AD=![]() ,∴AC2+DC2=20,AD2=20,∴AC2+DC2=AD2,∴△ACD是直角三角形且∠ACD=90°,∴tan∠DAC=
,∴AC2+DC2=20,AD2=20,∴AC2+DC2=AD2,∴△ACD是直角三角形且∠ACD=90°,∴tan∠DAC=![]() .
.
又∵∠DAC和∠OCB都是锐角,∴∠DAC=∠OCB,∴∠DAC+∠CAO=∠BCO+∠OCA,即∠DAB=∠ACB.
(3)令Q(x,y)且满足![]() ,A(-3,0),D(-1,4).∵△ADQ是以AD为底的等腰三角形,∴QD2=QA2,即
,A(-3,0),D(-1,4).∵△ADQ是以AD为底的等腰三角形,∴QD2=QA2,即![]() ,化简得:x-2+2y=0.
,化简得:x-2+2y=0.
由![]() ,解得:
,解得: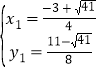 ,
,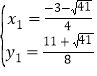 ,
,
∴点Q的坐标是(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】有这样一对数,如下表,第![]() 个数比第n个数大2(其中n是正整数)
个数比第n个数大2(其中n是正整数)
第1个 | 第2个 | 第3个 | 第4个 | 第5个 | …… |
a | b | c |
(1)第5个数表示为______;第7个数表示为_______.
(2)若第10个数是5,第11个数是8,第12个数为9,则a=______,b=_____,c=______.
(3)第2019个数可表示为________.
【题目】网上办公,手机上网已成为人们日常生活的一部分,我县某通信公司为普及网络使用,特推出以下两种电话拨号上网收费方式,用户可以任选其一.
收费方式一(计时制):0.05元/分;
收费方式二(包月制):50元/月(仅限一部个人电话上网);
同时,每一种收费方式均对上网时间加收0.02元/分的通信费.
某用户一周内的上网时间记录如下表:
日期 | 上网时间(分钟) |
星期一 | 35 |
星期二 | 40 |
星期三 | 33 |
星期四 | 50 |
星期五 | 34 |
星期六 | 40 |
星期日 | 48 |
(1)计算该用户一周内平均每天上网的时间.
(2)设该用户12月份上网的时间为![]() 小时,请你分别写出两种收费方式下该用户所支付的费用. (用含
小时,请你分别写出两种收费方式下该用户所支付的费用. (用含![]() 的代数式表示)
的代数式表示)
(3)如果该用户在一个月(30天)内,按(1)中的平均每天上网时间计算,你认为采用哪种方式支付费用较为合算?并说明理由.