题目内容
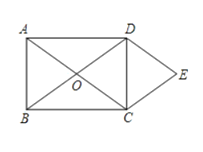
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD
(1)判断四边形OCED是什么特殊四边形?并证明你的结论
(2)当AB、AD满足什么条件时,四边形OCED是正方形?请说明理由。
【答案】(1)四边形OCED是菱形,理由见解析;(2)AB=AD,理由见解析
【解析】
(1)根据DE∥AC,CE∥BD.得出四边形OCED是平行四边形,根据矩形的性质求得OC=OD,即可判定四边形OCED是菱形;
(2)(2)先证明四边形OCED是平行四边形,由正方形的性质得出OA=OC=OB=OD,AC⊥BD,即可得出四边形OCED是正方形.
(1)四边形OCED是菱形.
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
在矩形ABCD中,OC=OD,
∴四边形OCED是菱形;
(2)AB=AD,理由如下:
∵CE∥BD,DE∥AC,
∴四边形OCED是平行四边形,
∵AB=AD,四边形ABCD是矩形,
∴OA=OC=OB=OD,AC⊥BD,
∴四边形OCED是正方形.

练习册系列答案
相关题目