题目内容
【题目】已知:正方形![]() ,
,![]() ,
,![]() .求证:
.求证:![]() .
.
【答案】见解析.
【解析】
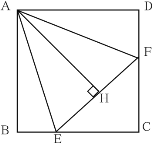
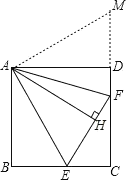
延长CD到M,使DM=BE,连接AM,证△ABE≌△ADM,推出∠DAM=∠BAE,AE=AM,求出∠FAM=∠EAF,证△EAF≌△MAF,推出EF=MF,S△EAF=S△MAF,根据三角形面积公式求出即可.
证明:延长CD到M,使DM=BE,连接AM,
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ADF=∠ADM=∠BAD=90°,
∵∠EAF=45°,
∴∠BAE+∠DAF=45°,
在△ABE和△ADM中,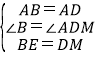 ,
,
∴△ABE≌△ADM,
∴∠DAM=∠BAE,AE=AM,
∴∠FAM=∠DAF+∠DAM=∠DAF+∠BAE=45°=∠EAF,
在△EAF和△MAF中,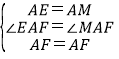 ,
,
∴△EAF≌△MAF,
∴EF=MF,S△EAF=S△MAF,
∴![]() EF×AH=
EF×AH=![]() MF×AD,
MF×AD,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目