ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌBDЪЧЁѕABCDЕФЖдНЧЯпЃЌABЁЭBDЃЌBD=8cmЃЌAD=10cmЃЌЖЏЕуPДгЕуDГіЗЂЃЌвд5cm/sЕФЫйЖШбиDAдЫЖЏЕНжеЕуAЃЌЭЌЪБЖЏЕуQДгЕуBГіЗЂЃЌбиелЯпBDЁЊDCдЫЖЏЕНжеЕуCЃЌдкBDЁЂDCЩЯЗжБ№вд8cm/sЁЂ6cm/sЕФЫйЖШдЫЖЏ.Й§ЕуQзїQMЁЭABЃЌНЛЩфЯпABгкЕуMЃЌСЌНгPQЃЌвдPQгыQMЮЊБпзїЁѕPQMN.ЩшЕуPЕФдЫЖЏЪБМфЮЊt(s)ЃЈt>0ЃЉЃЌЁѕPQMNгыЁѕABCDжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЈcm2ЃЉ.
ЃЈ1ЃЉAP=_______cmЃЈЭЌКЌtЕФДњЪ§ЪНБэЪОЃЉ.
ЃЈ2ЃЉЕБЕуNТфдкБпABЩЯЪБЃЌЧѓtЕФжЕ.
ЃЈ3ЃЉЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪН.
ЃЈ4ЃЉСЌНсNQЃЌЕБNQгыЁїABDЕФвЛБпЦНааЪБЃЌжБНгаДГіtЕФжЕ.
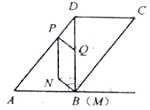
ЁОД№АИЁПЃЈ10-5tЃЉ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉжБНгЕУГіНсТлМДПЩЃЛ
ЃЈ2ЃЉЕБЕуNТфдкБпABЩЯЪБЃЌЫФБпаЮPNBQЮЊОиаЮЃЌЕУЕНЁїAPNЁзЁїADBЃЌгЩЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§НтД№МДПЩЃЛ
ЃЈ3ЃЉЗжШ§жжЧщПіЬжТлЃКЂйЕБPNдкЦНааЫФБпаЮФкВПЪБЃЌШчЭМ2ЃЌДЫЪБ![]() ЃЌЂкЕБNдкABЯТЗНЃЌQдкBDЩЯЪБЃЌДЫЪБ
ЃЌЂкЕБNдкABЯТЗНЃЌQдкBDЩЯЪБЃЌДЫЪБ![]() ЃЛЂлЕБNдкABЯТЗНЃЌQдкDCDЩЯЪБЃЌДЫЪБ
ЃЛЂлЕБNдкABЯТЗНЃЌQдкDCDЩЯЪБЃЌДЫЪБ![]() ЃЎ
ЃЎ
ЃЈ4ЃЉЗжШ§жжЧщПіЬжТлЃЎЂйЕБNQЁЮABЪБЃЌЂкЕБADЁЮNQЃЌЧвQдкBDЩЯЪБЃЌЂлЕБADЁЮNQЃЌЧвQдкDCЩЯЪБЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉЃЈ10-5tЃЉЃЛ
ЃЈ2ЃЉШчЭМЂйЃЌЕБЕуNТфдкБпABЩЯЪБЃЌЫФБпаЮPNBQЮЊОиаЮЃЎЁпPNЁЮDBЃЌЁрЁїAPNЁзЁїADBЃЌЁрAPЃКAD=PNЃКDBЃЌЁрЃЈ10Ѓ5tЃЉЃК10=8tЃК8ЃЌ120t=80ЃЌЁр![]() ЃЎ
ЃЎ

ЃЈ3ЃЉЗжШ§жжЧщПіЬжТлЃК
a)ШчЭМЂкЃЌЙ§ЕуPзїPEЁЭBDгкЕуEЃЌдђPE=3tЃЎ
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЎ
ЃЎ
b)ШчЭМЂлЃЌЙ§ЕуPзїPEЁЭBDгкЕуEЃЌдђPE=3tЃЌЩшPNНЛABгкЕуFЃЌдђ![]() ЃЎ
ЃЎ
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЎ
ЃЎ
c)ШчЭМЂмЃЌЕБ![]() ЪБЃЌPF=8-4tЃЌFB=3tЃЌPN=DB=QM=8ЃЌЁрFN=4tЃЌDQ=6(t-1)ЃЌЁрBM=DQ=6(t-1)ЃЎЁпЁЯGBM=ЁЯAЃЌЁЯDBA=ЁЯGMBЃЌЁрЁїBGMЁзЁїABDЃЌЁрGMЃКBM=DBЃКABЃЌНтЕУЃКGM=8t-8ЃЌЁрS=SЦНааЫФБпаЮPNMQ-SЁїFMN-SЁїBMG=8ЃЈ9t-6ЃЉЃ
ЪБЃЌPF=8-4tЃЌFB=3tЃЌPN=DB=QM=8ЃЌЁрFN=4tЃЌDQ=6(t-1)ЃЌЁрBM=DQ=6(t-1)ЃЎЁпЁЯGBM=ЁЯAЃЌЁЯDBA=ЁЯGMBЃЌЁрЁїBGMЁзЁїABDЃЌЁрGMЃКBM=DBЃКABЃЌНтЕУЃКGM=8t-8ЃЌЁрS=SЦНааЫФБпаЮPNMQ-SЁїFMN-SЁїBMG=8ЃЈ9t-6ЃЉЃ![]() ЁС4tЁСЃЈ9t-6ЃЉЃ
ЁС4tЁСЃЈ9t-6ЃЉЃ![]() ЁСЃЈ6t-6ЃЉЃЈ8t-8ЃЉ=
ЁСЃЈ6t-6ЃЉЃЈ8t-8ЃЉ=![]() ЃЎ
ЃЎ

злЩЯЫљЪіЃК 
ЃЈ4ЃЉЗжШ§жжЧщПіЬжТлЃЎ
ЂйЕБNQЁЮABЪБЃЌШчЭМ5ЃЌЙ§PзїPFЁЭBDгкFЃЌдђPF=3tЃЌDF=4tЃЌPN=FQ=BQ=8tЃЌЁрBD=8t+8t+4t=8ЃЌНтЕУЃК ![]() ЃЎ
ЃЎ
ЂкЕБADЁЮNQЃЌЧвQдкBDЩЯЪБЃЌШчЭМ6ЃЎЁпPNQDКЭPNBQЖМЪЧЦНааЫФБпаЮЃЌЁрPN=DQ=BQЃЌЁр8t+8t=8ЃЌНтЕУЃК ![]() ЃЎ
ЃЎ
ЂлЕБADЁЮNQЃЌЧвQдкDCЩЯЪБЃЌШчЭМ7ЃЌПЩвджЄУїЕБQгыCжиКЯЃЌМДжБЯпNQгыжБЯпBCжиКЯЪБЃЌТњзуЬѕМўЃЌШчЭМ8ЃЌДЫЪБDQ=AB=![]() =6ЃЌt=
=6ЃЌt=![]() =2ЃЎ
=2ЃЎ
злЩЯЫљЪіЃК ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ





 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ