题目内容
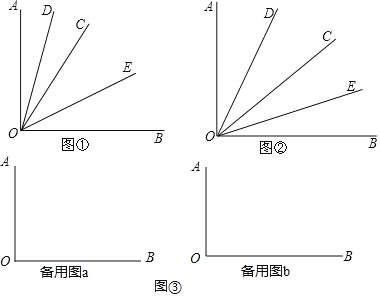
【题目】为了解某校九年级男生在体能测试的引体向上项目的情况，随机抽取了部分男生引体向上项目的测试成绩，绘制出如下的统计图①和图②．请根据相关信息，解答下列问题：
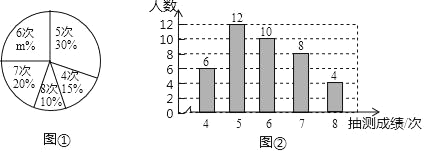
（Ⅰ）本次接受随机抽样调查的男生人数为 ，图①中m的值为 ；
（Ⅱ）求本次调查获取的样本数据的平均数、众数和中位数；
（Ⅲ）若规定引体向上6次及以上（含6次）为该项目良好，根据样本数据，估计该校320名九年级男生中该项目良好的人数．
【答案】(Ⅰ) 40；25；（Ⅱ）平均数为5.8次；众数为5；中位数为6；(Ⅲ)176名.
【解析】
（Ⅰ）用5次的人数除以5次的人数所占百分比即可得抽查的总人数；求出6次的人数与总人数的比即可得m的值；(Ⅱ)根据平均数、众数和中位数的定义求解即可；(Ⅲ)先求出6次及以上的学生所占的百分比，用320乘以这个百分比即可得答案.
（Ⅰ）12÷30%=40（名）；
×100%=25%，
∴m=25，
故答案为：40；25
(Ⅱ)平均数为：（6×4+12×5+10×6+8×7+4×8）÷40=5.8(次)
∵这组数据中，5出现了12次，出现次数最多，
∴这组数据的众数为5，
∵将这组数据从小到大排列，其中处于中间的两个数都是6，
∴
=6，即中位数为6，
(Ⅲ)6次及以上的学生人数为10+8+4=22（名）
∴
×320=176（名）
答：估计该校
名九年级男生中该项目良好的人数为176名.
阅读快车系列答案【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与
，所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, 
，2, 
，2
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+（____） |
5×5 | （________） |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.
【题目】一张长方形桌子可坐6人，按下图方式讲桌子拼在一起．
………
① ② ③
（1）观察图形，填写下表：
图形（n） | ② | ③ | …… | n |
坐的人数（人） | …… |
（2）一家餐厅有40张这样的长方形桌子，按照上图的方式每5张拼成1张大桌子，则40张桌子可拼成8张大桌子，共可坐多少人？
（3）在（2）中，若改为每8张桌子拼成1张大桌子，则共可坐多少人？
