题目内容
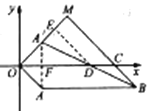
【题目】在平面直角坐标系
中，点
坐标为
，以原点
为顶点的四边形
是平行四边形，将边
沿
轴翻折得到线段
，连结
交线段
于点
.
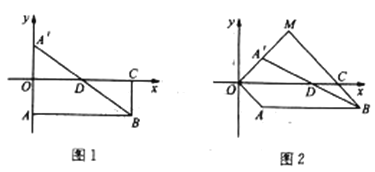
（1）如图1，当点
在
轴上，且其坐标为
.
①求所在直线的函数表达式；
②求证：点为线段的中点；
（2）如图2，当
时，，
的延长线相交于点
，试求
的值.（直接写出答案，不必说明理由）
【答案】（1）①
；②详见解析；（2）
【解析】
（1）①根据四边形
是平行四边形，得
，根据 
，
，得
.根据翻折得到线段
，得
.设直线
的函数表达式为
，利用待定系数法确定函数关系式即可求解；
②根据平行四边形的性质求证
，即可得点
为线段的中点.
（2）连接
交
轴于
点.证明为的中点，得出点为线段的中点，过点作
交
于点
，根据平行线分线段成比例定理得到
，还可得到等腰直角
，故
，求得.
解：（1）①∵四边形是平行四边形，
∴，
.
又∵点
落在
轴上，
∴
轴，∴
轴.
∵，，∴.
又∵边
沿轴翻折得到线段，
∴.
设直线的函数表达式为，
∴
，解得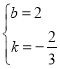
.
∴所在直线的函数表达式为.
②证明：∵四边形是平行四边形，∴，，
∴
.
∵边沿轴翻折得到线段，
∴
，∴
.
又∵
，∴，
∴
，即点为线段的中点.
（2）.
连接交轴于点.∴为的中点；
∴由（1）可得出点为线段的中点，
∵边沿轴翻折得到线段且
，
∴
，
.
∵，∴
.
过点作交于点，可得，得到等腰直角.
∴.
∴.
阅读快车系列答案
【题目】某商场在黄金周促销期间规定：商场内所有商品按标价的
打折出售；同时，当顾客在该商场消费打折后的金额满一定数额，还可按如下方案抵扣相应金额：
打折后消费金额 |
|
|
|
|
|
抵扣金额 | 20 | 30 | 40 | 50 |
|
说明：
表示在范围
中，可以取到a，不能取到b．
根据上述促销方法，顾客在该商场购物可以获得双重优惠：打折优惠与抵扣优惠．
例如：购买标价为900元的商品，则打折后消费金额为450元，获得的抵扣金额为30元，总优惠额为：
元，实际付款420元．
购买商品得到的优惠率
请问：
购买一件标价为500元的商品，顾客的实际付款是多少元？
购买一件商品，实际付款375元，那么它的标价为多少元？
请直接写出，当顾客购买标价为______元的商品，可以得到最高优惠率为______．
【题目】如图，在△ABC中，AB=4.41cm，BC=8.83cm，P是BC上一动点，连接AP，设P，C两点间的距离为xcm，P，A两点间的距离为ycm．（当点P与点C重合时，x的值为0）小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小东的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了x与y的几组值，如表：
x/cm | 0 | 0.43 | 1.00 | 1.50 | 1.85 | 2.50 | 3.60 | 4.00 | 4.30 | 5.00 | 5.50 | 6.00 | 6.62 | 7.50 | 8.00 | 8.83 |
y/cm | 7.65 | 7.28 | 6.80 | 6.39 | 6.11 | 5.62 | 4.87 | 4.47 | 4.15 | 3.99 | 3.87 | 3.82 | 3.92 | 4.06 | 4.41 |
（说明：补全表格时相关数值保留一位小数）
（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：当PA=PC时，PC的长度约为 cm．（结果保留一位小数）
