题目内容
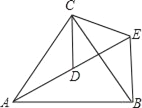
【题目】在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在射线BC上.
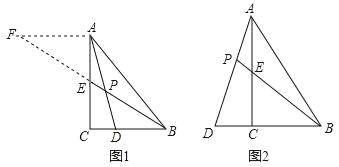
发现:如图1,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,过点A作AF∥BC,交BE的延长线于点F,求![]() 的值为.
的值为.
解决问题:如图2,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC=1:2.求![]() 的值.
的值.
应用:若CD=2,AC=6,求BP的值.
【答案】发现:![]() ;解决问题:
;解决问题:![]() ;应用:6.
;应用:6.
【解析】
发现:易证△AEF≌△CEB,则有AF=BC.设CD=k,则DB=2k,AF=BC=3k,由AF∥BC可得△APF∽△DPB,然后根据相似三角形的性质就可求出![]() 的值;
的值;
解决问题:过点A作AF∥DB,交BE的延长线于点F,设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.易证△AEF≌△CEB,则有EF=BE,AF=BC=2k.易证△AFP∽△DBP,然后根据相似三角形的性质就可求出![]() 的值;
的值;
应用:当CD=2时,可依次求出BC、AC、EC、EB、EF、BF的值,然后根据![]() 的值求出
的值求出![]() 的值,就可求出BP的值.
的值,就可求出BP的值.
发现:如图1中,∵AF∥BC,∴∠F=∠EBC.
∵∠AEF=∠BEC,AE=EC,∴△AEF≌△CEB(AAS),∴AF=BC.
设CD=k,则DB=2k,AF=BC=3k,由AF∥BC可得△APF∽△DPB,即可得到![]() =
=![]() =
=![]() .
.
故答案为:![]() ;
;
解决问题:
如图2中,过点A作AF∥DB,交BE的延长线于点F,如图,设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.
∵E是AC中点,∴AE=CE.
∵AF∥DB,∴∠F=∠1.
在△AEF和△CEB中,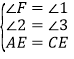 ,∴△AEF≌△CEB,∴EF=BE,AF=BC=2k.
,∴△AEF≌△CEB,∴EF=BE,AF=BC=2k.
∵AF∥DB,∴△AFP∽△DBP,∴![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
应用:
当CD=2时,BC=4,AC=6,∴EC=![]() AC=3,EB=
AC=3,EB=![]() =5,∴EF=BE=5,BF=10.
=5,∴EF=BE=5,BF=10.
∵![]() =
=![]() (已证),∴
(已证),∴![]() =
=![]() ,∴BP=
,∴BP=![]() BF=
BF=![]() ×10=6.
×10=6.
故答案为:6.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案