题目内容
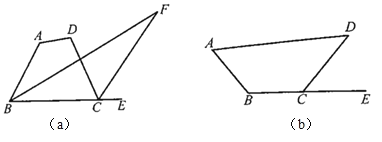
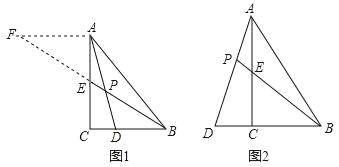
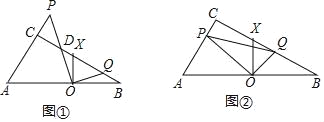
【题目】（1）如图①所示，∠ACB=∠POQ=∠XOB=90°．
①求证：∠POA=∠XOQ；
②判断△PAO和△QXO是否相似，如两个三角形相似请给出证明，如不相似，说明理由；
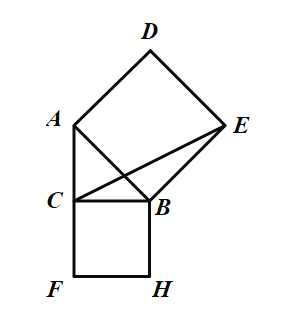
（2）如图②．在△ABC中，∠ACB=90°，∠CBA=30°，AO=BO，点P在AC上，点Q在BC上，且∠POQ=90°，XO⊥AB交BC于X，AC=4cm，AP=x（0＜x＜4），设△PCQ的面积为y，求y与x的函数关系式．
【答案】（1）①见解析；②△PAO∽△QOX；（2）y=﹣
x2+
（0＜x＜4）．
【解析】
（1）①根据同角的余角相等，即可证明；
②利用同角的余角相等，证明∠A=∠OXB即可解决问题；
（2）分两种情形分别求解即可：①如图当0＜x＜≤2时，作OM⊥AC于M，ON⊥BC于N．想办法求出CQ即可；②当2＜x＜4时，同法可得．
（1）①证明：∵∠POQ=∠XOB=∠XOA=90°，∴∠AOP+∠POX=∠XOQ+∠POX=90°，∴∠POA=∠XOQ．
②结论：△PAO∽△QOX．理由如下：
∵∠ACB=∠XOB=90°，∴∠A+∠B=90°，∠OXB+∠B=90°，∴∠A=∠OXB．
∵∠AOP=∠XOQ，∴△PAO∽△QOX．
（2）①如图当0＜x＜≤2时，作OM⊥AC于M，ON⊥BC于N．
在Rt△ACB中，∵∠B=30°，AC=4，∴AB=2AC=8，BC=4
．
∵∠C=∠ONB=90°，∴ON∥AC．
∵OA=OB，∴CN=BN，∴ON=
AC=2，同理可得：AM=CM，OM=BC=2．
∵∠POQ=∠MON=90°，∴∠POM=∠QON．
∵∠OMP=∠ONQ，∴△POM∽△QON，∴
=
=，∴QN=
（2﹣x），∴CQ=2﹣（2﹣x）=
+x，∴y=S△CPQ=CPCQ=（4﹣x）（+x）=﹣x2+．
②当2＜x＜4时，同法可得：y=（4﹣x）（+x）=﹣x2+．
综上所述：y=﹣x2+（0＜x＜4）．
