题目内容
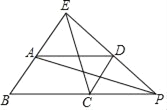
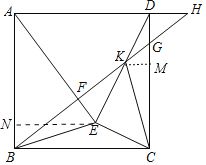
【题目】如图,在正方形ABCD中,以AB为腰向正方形内部作等腰△ABE,点G在CD上,且CG=3DG.连接BG并延长,与AE交于点F,与AD延长线交于点H.连接DE交BH于点K,连接CK.若AE2=BFBH,FG=![]() ,则S四边形EFKC=_____.
,则S四边形EFKC=_____.

【答案】![]()
【解析】
设DG=3a,CG=9a,作KM⊥CD于M,EN⊥AB于N,想办法求出线段KF、EF、KM、EN、FG,想办法用a的代数式表示四边形EFKC的面积,再求出a即可解决问题.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BAD=∠ADC=90°,
∵CG=3DG,
∴可以假设DG=3a,CG=9a,
则AB=AD=BC=CD=12a,
∴DG∥AB,
∴![]() ,
,
∴DH=4a,GH=5a,BH=20a,
∵AE2=BFBH,AE=AB,
∴AB2=BFBH,
∴![]() ,∵∠ABF=∠ABH,
,∵∠ABF=∠ABH,
∴△ABF∽HBA,
∴∠AFB=∠BAH=90°,
∴AF=![]() ,BF=
,BF=![]() a,
a,
∴FG=BH-BF-GH=![]() a,
a,
∵AE=AD,
∴∠ADE=∠AED,
∵∠ADE+∠GDK=90°,∠KEF+∠EKF=90°,∠EKF=∠GKD,
∴∠GDK=∠GKD,
∴GD=GK=3a,
作KM⊥CD于M,EN⊥AB于N,
∵![]() ,
,
∴KM=![]() a,
a,
∵△AFB≌△ANE,
∴EN=BF=![]() a,
a,
∴S四边形EFKC=S△EFK+S△ECK
=s△EFK+(S△CDE-S△CDK)
=![]() ×
×![]() a×
a×![]() a+(
a+(![]() ×12a×
×12a×![]() a-
a-![]() ×12a×
×12a×![]() a)
a)
=![]() a2,
a2,
∵FG=![]() a
a![]() ,
,
∴a=![]() ,
,
∴S四边形EFKC=![]() ,
,
故答案为![]() .
.

【题目】一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有3,4,5,x,甲,乙两人每次同时从袋中各随机取出1个小球,并计算2个小球上的数字之和.记录后将小球放回袋中搅匀,进行重复试验,试验数据如下表:
摸球总 次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为8”出 现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为8”出 现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列问题:
(1)如果试验继续进行下去,根据上表提供的数据,出现和为8的频率将稳定在它的概率附近,估计出现和为8的概率是________;
(2)如果摸出的2个小球上数字之和为9的概率是,那么x的值可以为7吗?为什么?