题目内容
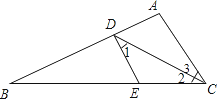
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D,且∠ACF=∠CBE,CG平分∠ACB交BD于点G,
(1)如图1,求证:CF=BG;
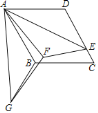
(2)如图2,延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,
求证:PB=CP+CF;
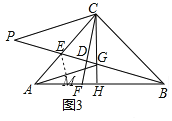
(3)如图3,在(2)间的条件下,当∠GAC=2∠FCH时,若S△AEG=3![]() ,BG=6,求AC的长.
,BG=6,求AC的长.

【答案】(1)见详解;(2)见详解;(3)3![]() +3
+3
【解析】
(1)根据ASA证明△BCG≌△CAF,则CF=BG;
(2)先证明△ACG≌△BCG,得∠CAG=∠CBE,再证明∠PCG=∠PGC,即可得出结论;
(3)作△AEG的高线EM,根据角的大小关系得出∠CAG=30°,根据面积求出EM的长,利用30°角的三角函数值依次求AE、EG、BE的长,所以CE=3+![]() ,根据线段的和得出AC的长.
,根据线段的和得出AC的长.
解::(1)∵∠ACB=90°,AC=BC,
∴∠A=45°,
∵CG平分∠ACB,
∴∠ACG=∠BCG=45°,
∴∠A=∠BCG,
在△BCG和△CAF中,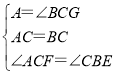 ,
,
∴△BCG≌△CAF(ASA),
∴CF=BG;
(2)∵PC∥AG,
∴∠PCA=∠CAG,
∵AC=BC,∠ACG=∠BCG,CG=CG,
∴△ACG≌△BCG,
∴∠CAG=∠CBE,
∵∠PCG=∠PCA+∠ACG=∠CAG+45°=∠CBE+45°,
∠PGC=∠GCB+∠CBE=∠CBE+45°,
∴∠PCG=∠PGC,
∴PC=PG,
∵PB=BG+PG,BG=CF,
∴PB=CF+CP;
过E作EM⊥AG,交AG于M,
∵S△AEG=![]() AGEM=3
AGEM=3![]() ,
,
由(2)得:△ACG≌△BCG,
∴BG=AG=6,
∴![]() ×6×EM=3
×6×EM=3![]() ,
,
EM=![]() ,
,
设∠FCH=x°,则∠GAC=2x°,
∴∠ACF=∠EBC=∠GAC=2x°,
∵∠ACH=45°,
∴2x+x=45,
x=15,
∴∠ACF=∠GAC=30°,
在Rt△AEM中,AE=2EM=2![]() ,
,
![]()
∴M是AG的中点,
∴AE=EG=2![]() ,
,
∴BE=BG+EG=6+2![]() ,
,
在Rt△ECB中,∠EBC=30°,
∴CE=![]() BE=3+
BE=3+![]() ,
,
∴AC=AE+EC=2![]() +3+
+3+![]() =3
=3![]() +3.
+3.

 名校课堂系列答案
名校课堂系列答案