题目内容
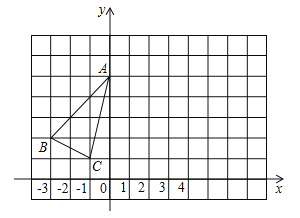
【题目】(1)如图 1 所示,△ ABC 和△ AEF 为等边三角形,点 E 在△ ABC 内部,且 E 到点 A、B、C 的距离分别为 3、4、5,求∠AEB 的度数.
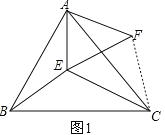
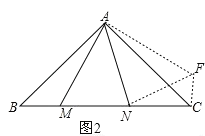
(2)如图 2,在△ ABC 中,∠CAB=90°,AB=AC,M、N 为 BC 上的两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°,得到△ACF.求证:MN![]() = NC
= NC![]() +BM
+BM![]() (提示:旋转前后的图形全等)
(提示:旋转前后的图形全等)
【答案】(1)∠AEB=150°;(2)见解析.
【解析】
(1)根据等边三角形的性质得出AE=AF=EF=3,AB=AC,∠AFE=60°,∠BAC=∠EAF=60°,求出∠BAE=∠CAF,证出△BAE≌△CAF,得出CF=BE=4,∠AEB=∠AFC,求出CE2=EF2+CF2,得出∠CFE=90°,即可得出结果;
(2)根据将△ABM绕A点逆时针旋转90°,得到△ACF,可知AM=AF,CF=BM,∠BAM=∠CAF,∠B=∠ACF,求出∠NAF=∠MAN,证出△MAN≌△FAN,得出MN=FN,求出∠FCN=90°,由勾股定理得出NF2=CF2+CN2即可解决问题.
解:(1)如图1所示:
∵△ABC和△AEF为等边三角形,
∴AE=AF=EF=3,AB=AC,∠AFE=60°,∠BAC=∠EAF=60°,
∴∠BAE=∠CAF=60°∠CAE,
在△BAE和△CAF中,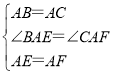 ,
,
∴△BAE≌△CAF(SAS),
∴CF=BE=4,∠AEB=∠AFC,
∴EF=3,CE=5,
∴CE2=EF2+CF2,
∴∠CFE=90°
∵∠AFE=60°,
∴∠AFC=90°+60°=150°,
∴∠AEB=∠AFC=150°;
(2)如图2所示:
∵将△ABM绕A点逆时针选择90°,得到△ACF,
∴AM=AF,CF=BM,∠BAM=∠CAF,∠B=∠ACF,
∵∠BAC=90°,∠MAN=45°,
∴∠NAF=∠CAN+∠FAC=∠CAN+∠BAM=90°45°=45°=∠MAN,
在△MAN和△FAN中,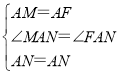 ,
,
∴△MAN≌△FAN(SAS),
∴MN=FN,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∵∠B=∠ACF,
∴∠ACF=45°,
∴∠FCN=90°,
由勾股定理得:NF2=CF2+CN2,
∵CF=BM,NF=MN,
∴MN2=NC2+BM2.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案