题目内容
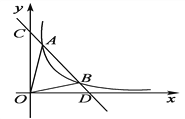
【题目】如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,边CO在x轴正半轴上,∠AOC=60°,反比例函数y=![]() (x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )
(x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )

A. 1 B. ![]() C. 2
C. 2![]() ﹣
﹣![]() D.
D. ![]() ﹣1
﹣1
【答案】C
【解析】
由菱形ABCO,∠AOC=60°,由解直角三角形可以设A(m,![]() m),又点A在反比例函数的图像上,带入可以求出A的坐标,进而可以求出OA的长度,即OC可求。再根据菱形ABCO,∠AOC=60°,可知∠BOC=30°,可设E(n,0),则D(n,
m),又点A在反比例函数的图像上,带入可以求出A的坐标,进而可以求出OA的长度,即OC可求。再根据菱形ABCO,∠AOC=60°,可知∠BOC=30°,可设E(n,0),则D(n,![]() n),带入反比例函数的解析式可以求出E点坐标,于是CE=OC-OE,可求.
n),带入反比例函数的解析式可以求出E点坐标,于是CE=OC-OE,可求.
解:∵四边形ABCO为菱形,∠AOC=60°,
∴可设A(m,![]() m),
m),
又∵A点在反比例函数y=![]() 上,
上,
∴![]() m2=2
m2=2![]() ,得m=
,得m=![]() (由题意舍m=-
(由题意舍m=-![]() ),
),
∴A(![]() ,
,![]() ),OA=2
),OA=2![]() ,
,
∴OC=OA=2![]() ,
,
又∵四边形ABCO为菱形,∠AOC=60°,OB为四边形ABCO的对角线,
∴∠BOC=30°,可设D(n,![]() n),则E(n,0),
n),则E(n,0),
∵D在反比例函数y=![]() 上,
上,
∴![]() n2=2
n2=2![]() ,解得n=
,解得n=![]() (由题意舍n= -
(由题意舍n= -![]() ),
),
∴E(![]() ,0),
,0),
∴OE=![]() ,
,
则有CE=OC-OE=2![]() -
-![]() .
.
故答案选C.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目