��Ŀ����
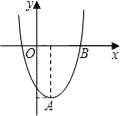
����Ŀ����ͼ����һ����Ƥ�����α�Ե��������״��MN=4�������߶��㴦����MN�ľ�����4��Ҫ����Ƥ�Ͻ���һ����ABCD��ʹ���ζ���B��C���ڱ�MN�ϣ�A��D�����������ϣ�
��1����ͼ�����ʵ�������ϵ���������߽���ʽ��
��2�������ABCD���ܳ�ΪL����C������Ϊ��m��0������L��m�Ĺ�ϵʽ����Ҫ��д�Ա���ȡֵ��Χ����
��3������������ȥ�ľ�����Ƥ���ܳ��ܷ����9.5����������9.5����˵�����ɣ�������9.5��������ֵ��

���𰸡���1��y=��x2+4x����2��L=��2m2+4m+8����3���ܵ���9.5����ʱm1=![]() ��m2=
��m2=![]() ��
��
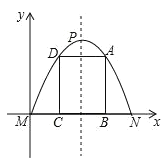
���������������: ��1������MN=4�������߶��㵽MN�ľ�����4dm���õ�N��4��0����P��2��4����������ú����Ľ���ʽ��
��2����BC��DC��m��ʾ����������L=2��BC+DC�����ɣ�
��3����L=9.5����L=��2m2+4m+8���ⷽ�̼��ɣ�
�������:
�⣺��1����MN=4dm�������߶��㵽MN�ľ�����4dm��
��N��4��0��������P��2��4����
�������ߵĽ���ʽΪ��y=a��x��2��2+4��
��N��4��0������ã�0=a��4��2��2+4��
��ã�a=��1��
�������ߵĽ���ʽΪ��y=����x��2��2+4��
���������ߵĽ���ʽΪ��y=��x2+4x��
��2����C��������m��0����
��BC=4��2m��DC�T��m2+4m��
��L=2��BC+DC��=��2m2+4m+8��
��3���ܵ���9.5��
��L=��2m2+4m+8=9.5��
��2m2��4m+1.5=0��
��ã�m1=![]() ��m2=
��m2=![]() ��
��
�㾦: ������Ҫ�������ô���ϵ��������κ�������ʽ�����κ�����ʵ��Ӧ�ã����κ�����һԪ���η��̵Ĺ�ϵ������Ĺؼ��ǽ�ʵ������ת������ѧ���⣮

����Ŀ����֪����![]() ������ͼ���ݺ���ͼ��ش��������⣺
������ͼ���ݺ���ͼ��ش��������⣺
��1���б�����㡢����
x | |||||
|
��2��![]() ���������Ƕ��٣�
���������Ƕ��٣�
��3��xȡ��ֵʱ��y��0��
��4��xȡ��ֵʱ����������x���ϻ��·���
��5��������![]() ��ֱ��y=k��Ψһ�Ľ��㣬��k=�� ����
��ֱ��y=k��Ψһ�Ľ��㣬��k=�� ����