题目内容
【题目】如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度( ![]() =1.7).
=1.7). 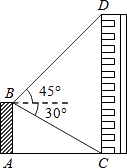
【答案】解:如图,过点B作BE⊥CD于点E,
根据题意,∠DBE=45°,∠CBE=30°.
∵AB⊥AC,CD⊥AC,
∴四边形ABEC为矩形.
∴CE=AB=12m.
在Rt△CBE中,cot∠CBE= ![]() ,
,
∴BE=CEcot30°=12× ![]() =12
=12 ![]() .
.
在Rt△BDE中,由∠DBE=45°,
得DE=BE=12 ![]() .
.
∴CD=CE+DE=12( ![]() +1)≈32.4.
+1)≈32.4.
答:楼房CD的高度约为32.4m.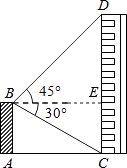
【解析】首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造关系式求解.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.

练习册系列答案
相关题目