Question

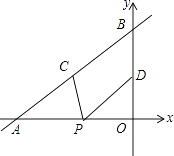
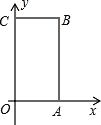
【题目】如图，长方形OABC中，O为直角坐标系的原点，A、C两点的坐标分别为（6，0）,（0，10），点B在第一象限内.

（1）写出点B的坐标，并求长方形OABC的周长；

（2）若有过点C的直线CD把长方形OABC的周长分成3:5两部分，D为直线CD与长方形的边的交点，求点D的坐标.

Answer 1

【答案】（1）点B的坐标为（6，10），长方形OABC的周长为32；（2）点D的坐标为（2，0）

【解析】试题分析：（1）由A、C的坐标得到OA，OC的长．由长方形的性质得到BC，AB的长，从而得到点B的坐标和长方形OABC的周长；

（2）由CD把长方形OABC的周长分为3：5两部分，得到被分成的两部分的长分别为12和20．然后分两种情况讨论：①当点D在AB上时，②当点D在OA上时．

试题解析：解：（1）∵A（6，0），C（0，10），∴OA=6，OC=10．

∵四边形OABC是长方形，∴BC=OA=6，AB=OC=10，∴点B的坐标为（6，10）．∵OC=10，OA=6，∴长方形OABC的周长为：2×（6+10）=32．

（2）∵CD把长方形OABC的周长分为3：5两部分，∴被分成的两部分的长分别为12和20．

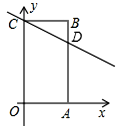
①当点D在AB上时，如图，AD=20-10-6=4，所以点D的坐标为（6，4）．

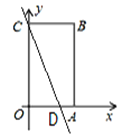
②当点D在OA上时，如图，OD=12-10=2，所以点D的坐标为（2，0）．