题目内容
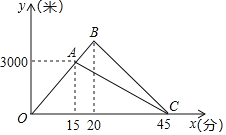
【题目】如图，在平面直角坐标系中，抛物线y＝﹣x2+3x+2与y轴交于点A，点B是抛物线的顶点，点C与点A是抛物线上关于对称轴对称的两个点，点D在x轴上运动，则四边形ABCD的两条对角线的长度之和的最小值为_____．
【答案】
【解析】
先将函数化为顶点式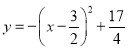
，所以顶点坐标
，对称轴为直线
，BD最小值为
，又点C与点A是抛物线上的两个对称点，对称轴为直线，所以C（3，2），AC＝3，因此四边形ABCD的两条对角线的长度之和AC+BD的最小值为
．
解：∵y＝﹣x2+3x+2＝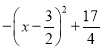
，
∴，对称轴为直线
∴当BD⊥x轴时，BD最小，BD＝
令x＝0，则y＝2，
∵C与点A是抛物线上关于对称轴对称的两个点，对称轴为直线，
∴C（3，2）
∴AC＝3，
四边形ABCD的两条对角线的长度之和AC+BD的最小值为
，
故答案为．
练习册系列答案
相关题目
【题目】焦作市教育局为调查全市教师的运动情况，结合现今流行的“微信运动”，随机调查了本市
名老师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表：
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
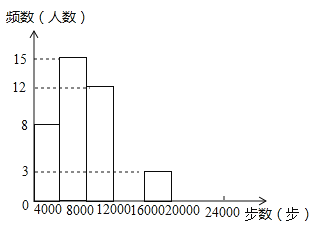
请根据以上信息，解答下列问题：
（1）写出
的值，并补全频数分布直方图；
（2）本市约有
名教师，结合调查的数据估计日行走步数超过
步（包含步）的教师有多少名？
（3）若在被调查的教师中，选取日行走步数超过
步（包含步）的两名教师与大家分享心得，求被选取的两名教师恰好都在
步（包含步）以上的概率．
