Question

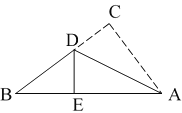
【题目】如图，在三角形纸片 ABC 中，AB=15cm，AC=9cm，BC=12cm， 现将边 AC 沿过点 A 的直线折叠，使它落在 AB 边上．若折痕交 BC 于点 D，点 C 落在点 E 处，你能求出 BD 的长吗？请写出求解过程．

Answer 1

【答案】BD=.

【解析】

先根据勾股定理得到∠C=∠DEA=90°，再根据折叠方法可得AC=AE，继而得到BE的长度,根据折叠方法可得CD=DE=（12-x）cm，则BD=xcm,在根据勾股定理得到BD的值.

由折叠可得AC=AE=9, DE=DC,∠C=∠DEA,

∴BE=AB-AC=6,

∵AB=15cm，AC=9cm，BC=12cm;

∴152=122+92,

∴∠C=∠DEA=90°，

设BD=x,DC=DE=12-x,

∵∠DEA=90°

∴∠DEB=90°

∴DE2+BE2=BD2,

∴BD=.