��Ŀ����
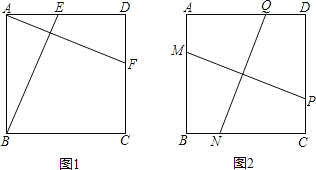
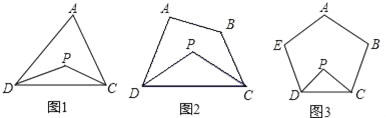
����Ŀ����1����֪����ͼ1��PΪ��ADC��һ�㣬DP��CP�ֱ�ƽ�֡�ADC�͡�ACD�������A=90������ô��P=______���������A=x�������P=____________��������ֱ���������к����ϣ�
��2����ͼ2��PΪ�ı���ABCD��һ�㣬DP��CP�ֱ�ƽ�֡�ADC�͡�BCD����̽����P���A+��B��������ϵ����д�����̽�����̣�
��3����ͼ3��PΪ�����ABCDE��һ�㣬DP��CP�ֱ�ƽ�֡�EDC�͡�BCD����ֱ��д����P���A+��B+��E��������ϵ��________________��
��4����PΪn����A1A2A3��An��һ�㣬PA1ƽ�֡�AnA1A2��PA2ƽ�֡�A1A2A3����ֱ��д����P���A3+A4+A5+����An��������ϵ��__________________________�����ú�n�Ĵ���ʽ��ʾ��
���𰸡������A=90������ô��P=135���������A=x�������P=��90+![]() ���� ��P=
���� ��P=![]() ����A+��B�� ��P=
����A+��B�� ��P=![]() ����A+��B+��E����90�� ��P=
����A+��B+��E����90�� ��P=![]() ����A3+��A4+��A5+����An������n��4����90��
����A3+��A4+��A5+����An������n��4����90��
��������
��1�����ݽ�ƽ���ߵĶ�����������ڽǺͶ�������ʽ�������
��2�����ݽ�ƽ���ߵĶ�����ı��ε��ڽǺͣ���ʽ�������
��3�����ݽ�ƽ���ߵĶ��������ε��ڽǺͣ���ʽ�������
��4�����ݽ�ƽ���ߵĶ����n���ε��ڽǺ�ʽ����ʽ�������
��1����DP��CP�ֱ�ƽ�֡�ADC�͡�ACD��
���PDC=![]() ��ADC����PCD=
��ADC����PCD=![]() ��ACD��
��ACD��
���DPC=180������PDC����PCD
=180����![]() ��ADC��
��ADC��![]() ��ACD
��ACD
=180����![]() ����ADC+��ACD��
����ADC+��ACD��
=180����![]() ��180������A��
��180������A��
=90��+ ![]() ��A��
��A��
�������A=90������ô��P=135���������A=x�������P=��90+![]() ������
������
��2����DP��CP�ֱ�ƽ�֡�ADC�͡�BCD��
���PDC=![]() ��ADC����PCD=
��ADC����PCD=![]() ��BCD��
��BCD��
���DPC=180������PDC����PCD
=180����![]() ��ADC��
��ADC��![]() ��BCD
��BCD
=180����![]() ����ADC+��BCD��
����ADC+��BCD��
=180����![]() ��360������A����B��
��360������A����B��
![]() ����A+��B����
����A+��B����
��3�������ABCDEF���ڽǺ�Ϊ����5��2��180��=540����
��DP��CP�ֱ�ƽ�֡�EDC�͡�BCD��
���PDC=![]() ��EDC����PCD=
��EDC����PCD=![]() ��BCD��
��BCD��
���P=180������PDC����PCD
=180����![]() ��EDC��
��EDC��![]() ��BCD
��BCD
=180����![]() ����EDC+��BCD��
����EDC+��BCD��
=180����![]() ��540������A����B����E��
��540������A����B����E��
=![]() ����A+��B+��E����90����
����A+��B+��E����90����
����P=![]() ����A+��B+��E����90����
����A+��B+��E����90����
��4��ͬ��1���ɵã���P=![]() ����A3+��A4+��A5+����An������n��4����90����
����A3+��A4+��A5+����An������n��4����90����
�ʴ�Ϊ����1�������A=90������ô��P=135���������A=x�������P=��90+![]() ������2����P=180������PDC����PCD=
������2����P=180������PDC����PCD=![]() ����A+��B����3����P=
����A+��B����3����P=![]() ����A+��B+��E����90����4����P=
����A+��B+��E����90����4����P=![]() ����A3+��A4+��A5+����An������n��4����90��
����A3+��A4+��A5+����An������n��4����90��