题目内容
【题目】已知二次函数y=﹣x2+2x+m.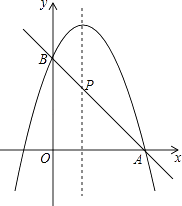
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
【答案】
(1)解:∵二次函数的图象与x轴有两个交点,
∴△=22+4m>0
∴m>﹣1;
(2)解:∵二次函数的图象过点A(3,0),
∴0=﹣9+6+m
∴m=3,
∴二次函数的解析式为:y=﹣x2+2x+3,
令x=0,则y=3,
∴B(0,3),
设直线AB的解析式为:y=kx+b,
∴ ![]() ,解得:
,解得: ![]() ,
,
∴直线AB的解析式为:y=﹣x+3,
∵抛物线y=﹣x2+2x+3,的对称轴为:x=1,
∴把x=1代入y=﹣x+3得y=2,
∴P(1,2).
(3)解:根据函数图象可知:x<0或x>3.
【解析】(1)根据已知二次函数的图象与x轴有两个交点,可得b2-4ac>0,建立不等式,求解即可。
(2)利用待定系数法,根据点A的坐标即可求出此抛物线的函数解析式,再由y=0,求出抛物线与y轴的交点坐标,再利用待定系数法求出直线AB的解析式,然后将抛物线和一次函数联立解方程组即可求得点P的坐标。
(3)观察函数图像,使一次函数值大于二次函数值,就是看一次函数图像高于二次函数的图像,即可得出x的取值范围。
【考点精析】关于本题考查的确定一次函数的表达式和抛物线与坐标轴的交点,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.

 阅读快车系列答案
阅读快车系列答案【题目】目前,我国大约有1.3亿高血压病患者,预防高血压不容忽视,“千帕![]() ”和“毫米汞柱
”和“毫米汞柱![]() ”都是表示血压的单位,请你根据表格提供的信息判断,下列各组换算正确的是( )
”都是表示血压的单位,请你根据表格提供的信息判断,下列各组换算正确的是( )
千帕 | … | 10 | 12 | 14 | … |
毫米汞柱 | … | 75 | 90 | 105 | … |
A.![]() B.
B.![]()
C.![]() D.
D.![]()