��Ŀ����
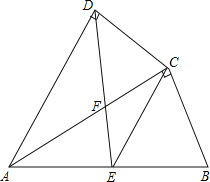
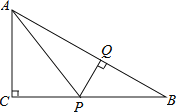
����Ŀ����Rt��ABC�У���C��90����P��BC���ϲ�ͬ��B��C��һ���㣬��P��PQ��AB������ΪQ������AP��
������⣺��1����֤����PBQ�ס�ABC��
����̽������2����AC��3��BC��4����BPΪ��ֵʱ����AQP������������ֵ��
��ɢ˼ά����3����Rt��ABC�У�����ֱ�DZ�BC��AC�����ϵʽBC��mAC���Ƿ����һ��m��ֵʹRt��AQP����Rt��ACPȫ�ȣ�Ҳ��Rt��BQPȫ�ȣ������ڣ���ֱ��д��m��ֵ���������ڣ�˵�����ɣ�
���𰸡���1������������2����BP��![]() ʱ����AQP���������ֵΪ
ʱ����AQP���������ֵΪ![]() ����3�����ڣ�m��
����3�����ڣ�m��![]() ʱ��Rt��AQP����Rt��ACPȫ�ȣ�Ҳ��Rt��BQPȫ�ȣ�
ʱ��Rt��AQP����Rt��ACPȫ�ȣ�Ҳ��Rt��BQPȫ�ȣ�
��������
��1�����ݴ�ֱ�Ķ������֪�����ɵ���PQB����C������B����B��Ȼ���������������ε��ж�����֤������PBQ�ס�ABC��
��2����BP��x�����ݹ��ɶ������AB��Ȼ��������������ε����ʣ��г�����ʽ���ֱ���x��ʾ��PQ��BQ��AQ��Ȼ����������ε������ʽ�������S��AQP��x�Ķ��κ�����ϵʽ��Ȼ�����ö��κ����Ķ���ʽ����ֵ���ɣ�
��3������ȫ�ȵ����ʿɵã�AQ��AC��AQ��QB���Ӷ��ó�AQ��QB��AC��Ȼ����ݹ��ɶ����ɵ�BC2��3AC2���Ӷ����m��ֵ.
��1��֤������PQ��AB��
���PQB��90����
���PQB����C���֡�B����B��
���PBQ�ס�ABC��
��2����BP��x��
�ߡ�C��90����AC��3��BC��4��
��AB��![]() ��
��![]() ��5��
��5��
�ߡ�PBQ�ס�ABC��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��
��ã�PQ��![]() x��BQ��
x��BQ��![]() x��
x��
��AQ��5��![]() x��
x��
��S��AQP��![]() ��AQ��PQ
��AQ��PQ
��![]() ����5��
����5��![]() x����
x����![]() x
x
����![]() x2+
x2+![]() x
x
����![]() ��x��
��x��![]() ��2+
��2+![]() ��
��
��BP��![]() ʱ����AQP���������ֵΪ
ʱ����AQP���������ֵΪ![]() ��
��
��3�����ڣ�
��Rt��AQP��Rt��ACP��
��AQ��AC��
��Rt��AQP��Rt��BQP��
��AQ��QB��
��AQ��QB��AC��
��Rt��ABC�У��ɹ��ɶ����� BC2��AB2��AC2
��BC2����2AC��2��AC2��
��BC2��3AC2��
��BC��![]() AC��
AC��
��m��![]() ʱ��Rt��AQP����Rt��ACPȫ�ȣ�Ҳ��Rt��BQPȫ�ȣ�
ʱ��Rt��AQP����Rt��ACPȫ�ȣ�Ҳ��Rt��BQPȫ�ȣ�