题目内容
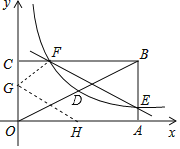
【题目】如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，OA＝8，点D为对角线OB的中点，若反比例函数y＝
在第一象限内的图象与矩形的边BC交于点F，与矩形边AB交于点E，反比例函数图象经过点D，且tan∠BOA＝
，设直线EF的表达式为y＝k2x+b．
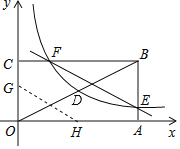
（1）求反比例函数表达式；
（2）直接写出直线EF的函数表达式_______；
（3）当x＞0时，直接写出不等式k2x+b＞的解集_____；
（4）将矩形折叠，使点O与点F重合，折痕与x轴正半轴交于点H，与y轴正半轴交于点G，直接写出线段OG的长______．
【答案】（1）y＝
；（2）y＝﹣
x+5；（3）2＜x＜8；（4）
．
【解析】
（1）利用正切的定义计算出AB得到B点坐标为（8，4），根据中点坐标公式可得到D（4，2），然后利用待定系数法确定反比例函数表达式；（2）利用反比例函数图象上点的坐标特征可确定E、F坐标，然后利用待定系数法求直线EF的解析式即可；（3）在第一象限内，根据E、F坐标写出一次函数图象在反比例函数图象上上方所对应的自变量的范围即可；（4）连接GF，如图，设OG＝t，则CG＝4﹣t，利用折叠的性质得到GF＝OG＝t，则利用勾股定理得到22+（4﹣t）2＝t2，然后解方程求出t即可得到OG的长．
（1）在Rt△AOB中，∵tan∠BOA＝
＝，
∴AB＝OA＝×8＝4，
∵OA=8，
∴点A坐标为（8，0），
∴B点坐标为（8，4），
∵点D为对角线OB的中点，
∴
，
，
∴点D坐标为（4，2），
把D（4，2）代入y＝
得k1＝4×2＝8，
∴反比例函数表达式为：y＝.
（2）当x＝8时，y＝＝1，
解得：y=1，
∴E（8，1），
当y＝4时，＝4，
解得：x＝2，
∴F（2，4），
把E（8，1），F（2，4）代入y＝k2x+b得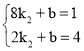
，
解得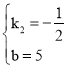
，
所以直线EF的解析式为：y＝﹣x+5.
故答案为：y＝﹣x+5
（3）∵E（8，1），F（2，4），
∴不等式k2x+b＞的解集为2＜x＜8.
故答案为：2＜x＜8
（4）如图，连接GF，设OG＝t，则CG＝4﹣t，
∵将矩形折叠，使点O与点F重合，
∴GF＝OG＝t，
∵F（2，4），
∴CF=2，
在Rt△CGF中，GF2=CG2+CF2，即22+（4﹣t）2＝t2，
解得：t＝，
∴OG的长为．
