题目内容
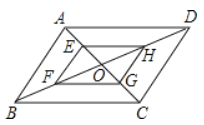
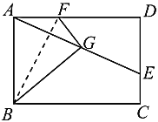
【题目】如图，矩形纸片
中，
，
，
是边
上一点，连接
．折叠该纸片，使点
落在上的
点，并使折痕经过点
，得到折痕
，点
在
上．若
，则
的长为（ ）
A.
B.4C.3D.2
【答案】C
【解析】
由矩形的性质可得AB=CD=6，AD=BC=8，∠BAD=∠D=90°，通过证明△ABF∽△DAE，可得
，即可求解．
解：设BF与AE交于点H，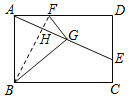
∵四边形ABCD为矩形，
∴AB=CD=6，AD=BC=8，∠BAD=∠D=90°，
由折叠及轴对称的性质可知，△ABF≌△GBF，BF垂直平分AG，
∴BF⊥AE，AH=GH，
∴∠BAH+∠ABH=90°，
又∵∠FAH+∠BAH=90°，
∴∠ABH=∠FAH，
又∵∠BAD=∠D=90°，
∴△ABF∽△DAE，
∴，
∴
，
故选：C．
练习册系列答案
相关题目
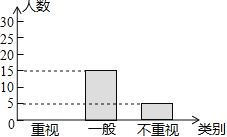
【题目】某教研机构为了了解初中生课外阅读名著的现状，随机抽取了某校50名初中生进行调查，依据相关数据绘制成了以下不完整的统计图，请根据图中信息解答下列问题：
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
（1）求表格中a，b的值；
（2）请补全统计图；
（3）若某校共有初中生2000名，请估计该校“重视课外阅读名著”的初中生人数．
