题目内容
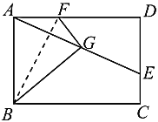
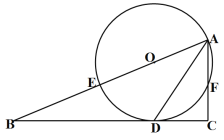
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A、D的⊙O分别交边AB、AC于点E、F.
(1)求证:BC是⊙O的切线;
(2)若BE=16,sinB=![]() ,求AF的长.
,求AF的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接OD,由AD为角平分线得到一对角相等,再由等边对等角得到一对角相等,等量代换得到内错角相等,进而得到OD与AC平行,得到OD与BC垂直,即可得证;
(2)连接EF,设圆的半径为r,由sinB的值,利用锐角三角函数定义求出r的值,由直径所对的圆周角为直角,得到EF与BC平行,得到sin∠AEF=sinB,进而求出AF的长即可.
(1)证明:如图,连接OD,
∵AD为∠BAC的角平分线,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODC=90°,
∴OD⊥BC,
∴BC为圆O的切线;
(2)在Rt△BOD中,sinB=![]() ,
,
设圆的半径为r,可得![]() ,
,
解得:r=10,
经检验,符合题意,
连接EF,
∵AE是直径
∴∠AFE=90°
∴EF∥BC
∴∠B=∠AEF
∴sinB=sin∠AEF=![]()
即![]()
∴AF=![]() .
.


【题目】某制药厂需要紧急生产一批能有效缓解“新冠肺炎”的药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量![]() (吨)是时间
(吨)是时间![]() (天)的一次函数,且满足如下表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本
(天)的一次函数,且满足如下表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本![]() (元)与时间
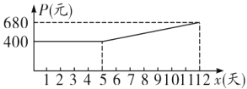
(元)与时间![]() (天)的关系满足如图所示的函数图象.
(天)的关系满足如图所示的函数图象.
时间 | 2 | 4 |
每天产量 | 24 | 28 |
(1)求药品每天的产量![]() (吨)与时间
(吨)与时间![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)当![]() 时,直接写出
时,直接写出![]() (元)与时间
(元)与时间![]() (天)的函数关系是
(天)的函数关系是![]() ;
;
(3)若这批药品的价格为1400元/吨,每天的利润设为![]() 元,求哪一天的利润最高,最高利润是多少?(利润
元,求哪一天的利润最高,最高利润是多少?(利润![]() 售价
售价![]() 成本)
成本)