题目内容
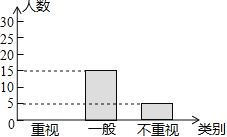
【题目】某教研机构为了了解初中生课外阅读名著的现状,随机抽取了某校50名初中生进行调查,依据相关数据绘制成了以下不完整的统计图,请根据图中信息解答下列问题:
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
(1)求表格中a,b的值;
(2)请补全统计图;
(3)若某校共有初中生2000名,请估计该校“重视课外阅读名著”的初中生人数.
【答案】(1)30,5;(2)补图见解析;(3)1200人.
【解析】
试题(1)由总人数结合条形统计图求出a与b的值即可;
(2)补全条形统计图,如图所示;
(3)求出“重视课外阅读名著”的初中生人数占的百分比,乘以2000即可得到结果.
试题解析:(1)根据题意得:b=5,a=50-(15+5)=30;
(2)补全条形统计图,如图所示:

(3)根据题意得:2000×![]() =1200(人),
=1200(人),
则该校“重视课外阅读名著”的初中生人数约有1200人.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
【题目】某制药厂需要紧急生产一批能有效缓解“新冠肺炎”的药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量![]() (吨)是时间
(吨)是时间![]() (天)的一次函数,且满足如下表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本
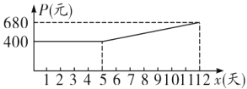
(天)的一次函数,且满足如下表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本![]() (元)与时间
(元)与时间![]() (天)的关系满足如图所示的函数图象.
(天)的关系满足如图所示的函数图象.
时间 | 2 | 4 |
每天产量 | 24 | 28 |
(1)求药品每天的产量![]() (吨)与时间
(吨)与时间![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)当![]() 时,直接写出
时,直接写出![]() (元)与时间
(元)与时间![]() (天)的函数关系是
(天)的函数关系是![]() ;
;
(3)若这批药品的价格为1400元/吨,每天的利润设为![]() 元,求哪一天的利润最高,最高利润是多少?(利润
元,求哪一天的利润最高,最高利润是多少?(利润![]() 售价
售价![]() 成本)
成本)