ЬтФПФкШн
ЁОЬтФПЁПЙЄНГжЦзїФГжжН№ЪєЙЄОпвЊНјааВФСЯьбЩеКЭЖЭдьСНИіЙЄађЃЌМДашвЊНЋВФСЯЩеЕН800ЁцЃЌШЛКѓЭЃжЙьбЩеНјааЖЭдьВйзїЃЌОЙ§![]() ЪБЃЌВФСЯЮТЖШНЕЮЊ600ЁцЃЎШчЭМЃЌьбЩеЪБЮТЖШ
ЪБЃЌВФСЯЮТЖШНЕЮЊ600ЁцЃЎШчЭМЃЌьбЩеЪБЮТЖШ![]() гыЪБМф
гыЪБМф![]() ГЩвЛДЮКЏЗѓЙиЯЕЃКЖЭдьЪБЃЌЮТЖШ
ГЩвЛДЮКЏЗѓЙиЯЕЃКЖЭдьЪБЃЌЮТЖШ![]() гыЪБМф
гыЪБМф![]() ГЩЗДБШР§КЏЪ§ЙиЯЕЁЃвбжЊИУВФСЯГѕЪМЮТЖШЪЧ32ЁцЃЎ
ГЩЗДБШР§КЏЪ§ЙиЯЕЁЃвбжЊИУВФСЯГѕЪМЮТЖШЪЧ32ЁцЃЎ
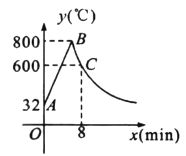
ЃЈ1ЃЉЗжБ№ЧѓГіВФСЯьбЩеКЭЖЭдьЪБ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧваДГіздБфСП
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧваДГіздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉИљОнЙЄвевЊЧѓЃЌЕБВФСЯЮТЖШЕЭгк400ЁцЪБЃЌаыЭЃжЙВйзїЃЎФЧУДЖЭдьЕФВйзїЪБМфзюЖргаЖрГЄЃПЃЎ
ЃЈ3ЃЉШчЙћМгЙЄУПИіСуМўашвЊЖЭдь12ЗжжгЃЌВЂЧвЕБВФСЯЮТЖШЕЭгк400ЁцЪБЃЌашвЊжиаТьбЩеЃЎЭЈЙ§МЦЫуЫЕУїМгЙЄЕквЛИіСуМўЃЌвЛЙВашвЊЖрЩйЗжжгЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉЖЭдьвЛДЮВйзїЪБМфЮЊ6ЗжжгЃЛЃЈ3ЃЉМгЙЄЕквЛИіСуМўвЛЙВашвЊ
ЃЛЃЈ2ЃЉЖЭдьвЛДЮВйзїЪБМфЮЊ6ЗжжгЃЛЃЈ3ЃЉМгЙЄЕквЛИіСуМўвЛЙВашвЊ![]() ЗжжгЃЎ
ЗжжгЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЖЭдьЪБЃЌЩш![]() ЃЌЧѓГіЗДБШР§КЏЪ§НтЮіЪНЃЌЕБ
ЃЌЧѓГіЗДБШР§КЏЪ§НтЮіЪНЃЌЕБ![]() ЪБЃЌЧѓГіЕуBЕФзјБъЃЌШЛКѓЩшьбЩеЪБвЛДЮКЏЪ§ЮЊ
ЪБЃЌЧѓГіЕуBЕФзјБъЃЌШЛКѓЩшьбЩеЪБвЛДЮКЏЪ§ЮЊ![]() ЃЌДњШыЕуBзјБъЧѓГівЛДЮКЏЪ§НтЮіЪНЃЌВЂЧѓГівЛДЮКЏЪ§КЭЗДБШР§КЏЪ§здБфСП
ЃЌДњШыЕуBзјБъЧѓГівЛДЮКЏЪ§НтЮіЪНЃЌВЂЧѓГівЛДЮКЏЪ§КЭЗДБШР§КЏЪ§здБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉАб![]() ДњШыЗДБШР§КЏЪ§НтЮіЪНЃЌЧѓГіxЕФжЕдйМѕШЅЕк6ЗжжгПЊЪМЖЭдьЃЌМДПЩЕУГіД№АИЃЛ
ДњШыЗДБШР§КЏЪ§НтЮіЪНЃЌЧѓГіxЕФжЕдйМѕШЅЕк6ЗжжгПЊЪМЖЭдьЃЌМДПЩЕУГіД№АИЃЛ
ЃЈ3ЃЉЕквЛДЮЖЭдьашвЊ6ЗжжгЃЌЕкЖўДЮьбЩеЪЧДг400ЁцьбЩеЕН800ЁцЃЌЕБ![]() ЪБЃЌДњШывЛДЮКЏЪ§НтЮіЪНЃЌЧѓГіьбЩеЕФЪБМфЃЌМДПЩЧѓГіМгЙЄЕквЛИіСуМўЫљашЕФЪБМфЃЎ
ЪБЃЌДњШывЛДЮКЏЪ§НтЮіЪНЃЌЧѓГіьбЩеЕФЪБМфЃЌМДПЩЧѓГіМгЙЄЕквЛИіСуМўЫљашЕФЪБМфЃЎ
(1)ВФСЯЖЭдьЪБЃЌЩш![]() ЃЌгЩЬтвтЕУ
ЃЌгЩЬтвтЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрЕу![]() ЕФзјБъЮЊ(6ЃЌ800)ЃЌВФСЯьбЩеЪБЃЌЩш
ЕФзјБъЮЊ(6ЃЌ800)ЃЌВФСЯьбЩеЪБЃЌЩш![]() ЃЌ
ЃЌ
гЩЬтвтЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрВФСЯьбЩеЪБЃЌ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЮЊ
ЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ЃЎ
ЃЎ
ВФСЯЖЭдьЪБ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЮЊЃЛ
ЕФКЏЪ§ЙиЯЕЪНЮЊЃЛ![]()
(2)Аб![]() ДњШы
ДњШы![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
![]() ЃЌМД:ЖЭдьвЛДЮВйзїЪБМфЮЊ6ЗжжгЃЎ
ЃЌМД:ЖЭдьвЛДЮВйзїЪБМфЮЊ6ЗжжгЃЎ
(3)ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЁрЖЭдьУПИіСуМўашвЊьбЩеСНДЮЃЌЕквЛДЮьбЩеашвЊ6ЗжжгЃЌЕкЖўДЮьбЩеДг400ЁцьбЩеЕН800ЁцЃЌ
ЕБ![]() ЪБЃЌДњШы
ЪБЃЌДњШы![]() ЃЌ
ЃЌ![]() ЃЌгУЪБ
ЃЌгУЪБ![]() ЃЌ
ЃЌ
ЁрМгЙЄЕквЛИіСуМўвЛЙВашвЊ![]() ЗжжгЃЎ
ЗжжгЃЎ

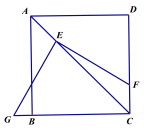
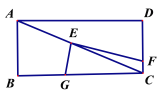
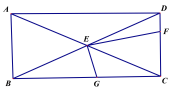
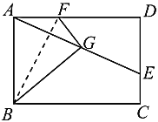
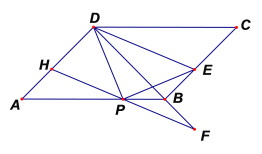
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAEЦНЗжЁЯBACНЛBCгкЕуEЃЌDЪЧABБпЩЯвЛЖЏЕуЃЌСЌНгCDНЛAEгкЕуPЃЌСЌНгBPЃЎвбжЊAB =6cmЃЌЩшBЃЌDСНЕуМфЕФОрРыЮЊxcmЃЌBЃЌPСНЕуМфЕФОрРыЮЊy1cmЃЌAЃЌPСНЕуМфЕФОрРыЮЊy2cmЃЎ
аЁУїИљОнбЇЯАКЏЪ§ЕФОбщЃЌЗжБ№ЖдКЏЪ§y1ЃЌy2ЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎ
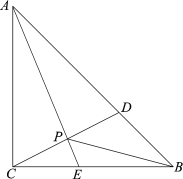
ЯТУцЪЧаЁУїЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећ:
ЃЈ1ЃЉАДееЯТБэжаздБфСПxЕФжЕНјааШЁЕуЁЂЛЭМЁЂВтСПЃЌЗжБ№ЕУЕНСЫy1ЃЌ![]() гыxЕФМИзщЖдгІжЕЃК
гыxЕФМИзщЖдгІжЕЃК
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 2.49 | 2.64 | 2.88 | 3.25 | 3.80 | 4.65 | 6.00 |
y2/cm | 4.59 | 4.24 | 3.80 | 3.25 | 2.51 | 0.00 |
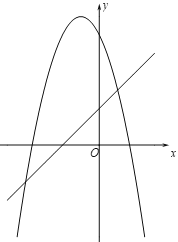
ЃЈ2ЃЉдкЭЌвЛЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГіВЙШЋКѓЕФБэжаИїзщЪ§жЕЫљЖдгІЕФЕу(xЃЌy1)ЃЌ(xЃЌ![]() )ЃЌВЂЛГіКЏЪ§y1ЃЌ
)ЃЌВЂЛГіКЏЪ§y1ЃЌ![]() ЕФЭМЯѓЃЛ
ЕФЭМЯѓЃЛ

ЃЈ3ЃЉНсКЯКЏЪ§ЭМЯѓЃЌЛиД№ЯТСаЮЪЬтЃК
ЂйЕБAP=2BDЪБЃЌAPЕФГЄЖШдМЮЊ cmЃЛ
ЂкЕБBPЦНЗжЁЯABCЪБЃЌBDЕФГЄЖШдМЮЊ cmЃЎ
ЁОЬтФПЁПФГжЦвЉГЇашвЊНєМБЩњВњвЛХњФмгааЇЛКНтЁАаТЙкЗЮбзЁБЕФвЉЦЗЃЌвЊЧѓБиаыдк12ЬьЃЈКЌ12ЬьЃЉФкЭъГЩЃЎЮЊСЫМгПьЩњВњЃЌГЕМфВЩШЁЙЄШЫМгАрЃЌЛњЦїВЛЭЃЕФЩњВњЗНЪНЃЌетбљУПЬьвЉЦЗЕФВњСП![]() ЃЈЖжЃЉЪЧЪБМф
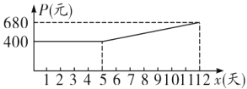
ЃЈЖжЃЉЪЧЪБМф![]() ЃЈЬьЃЉЕФвЛДЮКЏЪ§ЃЌЧвТњзуШчЯТБэжаЫљЖдгІЕФЪ§СПЙиЯЕЃЎгЩгкЛњЦїИККЩдЫзЊВњЩњЫ№КФЃЌЦНОљЩњВњУПЖжвЉЦЗЕФГЩБО
ЃЈЬьЃЉЕФвЛДЮКЏЪ§ЃЌЧвТњзуШчЯТБэжаЫљЖдгІЕФЪ§СПЙиЯЕЃЎгЩгкЛњЦїИККЩдЫзЊВњЩњЫ№КФЃЌЦНОљЩњВњУПЖжвЉЦЗЕФГЩБО![]() ЃЈдЊЃЉгыЪБМф
ЃЈдЊЃЉгыЪБМф![]() ЃЈЬьЃЉЕФЙиЯЕТњзуШчЭМЫљЪОЕФКЏЪ§ЭМЯѓЃЎ
ЃЈЬьЃЉЕФЙиЯЕТњзуШчЭМЫљЪОЕФКЏЪ§ЭМЯѓЃЎ
ЪБМф | 2 | 4 |
УПЬьВњСП | 24 | 28 |
ЃЈ1ЃЉЧѓвЉЦЗУПЬьЕФВњСП![]() ЃЈЖжЃЉгыЪБМф
ЃЈЖжЃЉгыЪБМф![]() ЃЈЬьЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈЬьЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌжБНгаДГі
ЪБЃЌжБНгаДГі![]() ЃЈдЊЃЉгыЪБМф
ЃЈдЊЃЉгыЪБМф![]() ЃЈЬьЃЉЕФКЏЪ§ЙиЯЕЪЧ
ЃЈЬьЃЉЕФКЏЪ§ЙиЯЕЪЧ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШєетХњвЉЦЗЕФМлИёЮЊ1400дЊ/ЖжЃЌУПЬьЕФРћШѓЩшЮЊ![]() дЊЃЌЧѓФФвЛЬьЕФРћШѓзюИпЃЌзюИпРћШѓЪЧЖрЩйЃПЃЈРћШѓ
дЊЃЌЧѓФФвЛЬьЕФРћШѓзюИпЃЌзюИпРћШѓЪЧЖрЩйЃПЃЈРћШѓ![]() ЪлМл
ЪлМл![]() ГЩБОЃЉ
ГЩБОЃЉ