题目内容
【题目】如图，已知矩形ABCD的长AB为5，宽BC为4，E是BC边上的一个动点，AE⊥EF，EF交CD于点F．设BE=x，FC=y，则点E从点B运动到点C时，能表示y关于x的函数关系的大致图像是（ ）
A.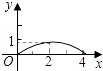
B.
C.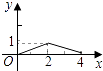
D.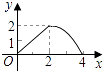
【答案】A
【解析】解：∵BC=4，BE=x，
∴CE=4﹣x．
∵AE⊥EF，
∴∠AEB+∠CEF=90°，
∵∠CEF+∠CFE=90°，
∴∠AEB=∠CFE．
又∵∠B=∠C=90°，
∴Rt△AEB∽Rt△EFC，
∴ 
，
即 
，
整理得：y= 
（4x﹣x2）=﹣ （x﹣2）2+ 
∴y与x的函数关系式为：y=﹣ （x﹣2）2+ （0≤x≤4）
由关系式可知，函数图像为一段抛物线，开口向下，顶点坐标为（2， ），对称轴为直线x=2．
故选：A．
利用三角形相似求出y关于x的函数关系式，根据函数关系式进行分析求解．
练习册系列答案
相关题目
