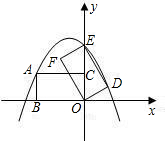
题目内容
一条抛物线y=
x2+mx+n经过点(0,
)与(4,
).
(1)求这条抛物线的解析式,并写出它的顶点坐标;
(2)现有一半径为1,圆心P在抛物线上运动的动圆,当⊙P与坐标轴相切时,求圆心P的坐标.

| 1 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
(1)求这条抛物线的解析式,并写出它的顶点坐标;
(2)现有一半径为1,圆心P在抛物线上运动的动圆,当⊙P与坐标轴相切时,求圆心P的坐标.

(1)由抛物线过(0,
),(4,
)两点,
得
,
解得
.
∴抛物线的解析式是:y=
x2-x+
,(3分)
由y=
x2-x+
=
(x-2)2+
,得抛物线的顶点(2,
);
(2)设点P的坐标为(x0,y0)
①当圆P与y轴相切时,有|x0|=1,
∴x0=±1
由x0=1,得y0=
×1-1+
=
由x0=-1,得y0=
×(-1)2-(-1)+
=
此时,点P的坐标为P1(1,
),P2(-1,
);
②当圆P与x轴相切时,有|y0|=1
∵抛物线的开口向上,顶点在x轴的上方,y0>0,∴y0=1
由y0=1,得
x02-x0+
=1
解得x0=2±
此时,点P的坐标为P3(2-
,1),P4(2+
,1)
综上所述,圆心P的坐标为P1(1,
),P2(-1,
),P3(2-
,1),P4(2+
,1).
| 3 |
| 2 |
| 3 |
| 2 |
得
|
解得
|
∴抛物线的解析式是:y=
| 1 |
| 4 |
| 3 |
| 2 |
由y=
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)设点P的坐标为(x0,y0)
①当圆P与y轴相切时,有|x0|=1,
∴x0=±1
由x0=1,得y0=
| 1 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
由x0=-1,得y0=
| 1 |
| 4 |
| 3 |
| 2 |
| 11 |
| 4 |
此时,点P的坐标为P1(1,
| 3 |
| 4 |
| 11 |
| 4 |
②当圆P与x轴相切时,有|y0|=1
∵抛物线的开口向上,顶点在x轴的上方,y0>0,∴y0=1
由y0=1,得
| 1 |
| 4 |
| 3 |
| 2 |
解得x0=2±
| 2 |
此时,点P的坐标为P3(2-
| 2 |
| 2 |
综上所述,圆心P的坐标为P1(1,
| 3 |
| 4 |
| 11 |
| 4 |
| 2 |
| 2 |

练习册系列答案
相关题目

 应点为点D,抛物线y=ax2+bx+c过点A,E,D.
应点为点D,抛物线y=ax2+bx+c过点A,E,D.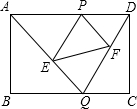 最大值为多少?
最大值为多少?