题目内容
【题目】如图,在菱形ABCD中,AB=BD=4,E为AB的中点,P为AC上一个动点,则EP+BP的最小值为_____.

【答案】![]()
【解析】
连结DE交AC于点P,连结BP,根据菱形的性质推出AO是BD的垂直平分线,推出PE+PB=PE+PD=DE且值最小,根据勾股定理求出DE的长即可.
如图,设AC,BD相交于O,连结DE交AC于点P,连结BP,
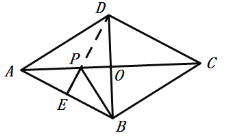
∵四边形ABCD是菱形,
∴AC⊥BD,且DO=BO,即AO是BD的垂直平分线,
∴PD=PB,
∴PE+PB=PE+PD=DE且值最小,
∵E是AB的中点,EM⊥BD,
∵四边形ABCD是菱形,且AB=BD=4,E为AB的中点,
∴△ABD是等边三角形,AE=BE=2,
∴DE=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目