题目内容
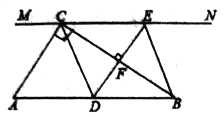
【题目】如图:在Rt△ABC中,∠ACB=90°,过点C的直线MN//AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连结CD,BE.
(1)求点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由.
(2)在(1)的条件下,当∠A= 时,四边形BECD是正方形.说明你的理由.
【答案】(1)平行四边形BECD是菱形,理由见解析;(2)45°
【解析】
(1)先证明AC∥DE,得出四边形BECD是平行四边形,再“根据直角三角形斜边上的中线等于斜边的一半”证出CD=BD,得出四边形BECD是菱形;
(2)先求出∠ABC=45°,再根据菱形的性质求出∠DBE=90°,即可证出结论.
(1)当点D是AB的中点时,四边形BECD是菱形;理由如下:
∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
∵D为AB中点,
∴AD=BD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=![]() AB=BD,
AB=BD,
∴四边形BECD是菱形;
(2)当∠A=45°时,四边形BECD是正方形;理由如下:
∵∠ACB=90°,∠A=45°,
∴∠ABC=45°,
∵四边形BECD是菱形,
∴∠ABC=![]() ∠DBE,
∠DBE,
∴∠DBE=90°,
∴四边形BECD是正方形.
故答案为:45°.

 教材全解字词句篇系列答案
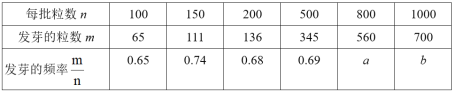
教材全解字词句篇系列答案【题目】某商场计划购进冰箱、彩电进行销售.相关信息如下表:
进价(元/台) | 售价(元/台) | |
冰箱 |
| 2500 |
彩电 |
| 2000 |
(1)若商场用80000元购进冰箱的数量与用64000元购进彩电的数量相等,求表中a的值.
(2)为了满足市场需要求,商场决定用不超过9万元采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的![]() .
.
①该商场有哪几种进货方式?
②若该商场将购进的冰箱、彩电全部售出,获得的最大利润为w元,请用所学的函数知识求出w的值.