��Ŀ����
����Ŀ���ۺ���̽��
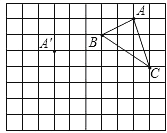
��ͼ1��ʾ��ֱ��y=x+c��x�ύ�ڵ�A����4��0������y�ύ�ڵ�C��������y=��x2+bx+c������A��C��
��1���������ߵĽ���ʽ
��2����E�������ߵĶԳ����ϣ���CE+OE����Сֵ��
��3����ͼ2��ʾ��M���߶�OA����һ�����㣬����M��ֱ��x���ֱ����ֱ��AC�������߷ֱ��ڵ�P��N
������C��P��NΪ���������������APM���ƣ�����CPN�����Ϊ�� ����
������Pǡ�����߶�MN���е㣬��F��ֱ��AC��һ�����㣬������ƽ�����Ƿ���ڵ�D��ʹ�Ե�D��F��P��MΪ������ı��������Σ������ڣ���ֱ��д����D�����ꣻ�������ڣ���˵�����ɣ�
ע�����κ���y=ax2+bx+c��a��0���Ķ�������Ϊ����![]() ��
��![]() ��
��

���𰸡���1��y=��x2��3x+4����2��CE+OE����СֵΪ5����3��![]() ��4����������PF=FMʱ����D��MN��ֱƽ�����ϣ���D��
��4����������PF=FMʱ����D��MN��ֱƽ�����ϣ���D��![]() ������PM=PFʱ�����������ʵ�D����Ϊ����1+
������PM=PFʱ�����������ʵ�D����Ϊ����1+![]() ��
��![]() ������1��
������1��![]() ����
����![]() ������MP=MFʱ��M��D����ֱ��y=��x+4�Գƣ���D����Ϊ����4��3��.
������MP=MFʱ��M��D����ֱ��y=��x+4�Գƣ���D����Ϊ����4��3��.
��������
��1������֪������������ʽ��
��2��ȡ��C���������ߵĶԳ���ֱ��l�ĶԳƵ�C����������֮���߶���̣���Сֵ�ɵã�
��3��������֪��ע�����������εķ������ۣ�
�����M���꣬���P���꣮ע���������ɵ����������Եױ�����ֱ��Ϊ�Գ���ԳƵõ��ģ����⼴Ϊ�о���CPNΪ���������ε������
�⣺��1����A����4��0������y=x+c
��c=4
��A����4��0����c=4����y=��x2+bx+c
��b=��3
�������߽���ʽΪy=��x2��3x+4
��2������C���������ߵĶԳ���ֱ��l�ĶԳƵ�C�䣬��OC�䣬��ֱ��l�ڵ�E��
��CE����ʱCE+OE��ֵ��С��
�������߶Գ���λ����x=��![]()
��CC��=3
�ɹ��ɶ���OC��=5
��CE+OE����СֵΪ5
��3���ٵ���CNP�ס�AMPʱ��

��CNP=90�㣬��NC���������߶Գ���Գ�
��NC=NP=3
���CPN�����Ϊ![]()
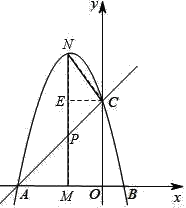
����CNP�ס�MAPʱ
����֪��NCPΪ����ֱ�������Σ���NCP=90��
����C��CE��MN�ڵ�E�����M����Ϊ��a��0��
��EP=EC=��a��
��N��a����a2��3a+4����MP=��a2��3a+4������2a��=��a2��a+4
��P��a����a2��a+4��
����y=x+4
���a=��2
���CPN�����Ϊ4
�ʴ�Ϊ��![]() ��4
��4
�ڴ���
��M������a��0��
��N��a����a2��3a+4��
��P��������a��![]() ��
��
�ѵ�P�������y=��x+4
���a1=��4����ȥ����a2=��1
��PF=FMʱ����D��MN��ֱƽ�����ϣ���D��![]() ��
��![]() ��
��
��PM=PFʱ�����������ʵ�D����Ϊ����1+![]() ��
��![]() ������1��
������1��![]() ����
����![]() ��
��
��MP=MFʱ��M��D����ֱ��y=��x+4�Գƣ���D����Ϊ����4��3��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�