题目内容
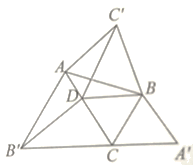
【题目】如图所示,在△ABC中,已知∠DBC=60°,AC>BC,又△ABC'、△BCA'、△CAB'都是△ABC形外的等边三角形,而点D在AC上,且BC=DC
(1)证明:△C'BD≌△B'DC
(2)证明:△AC'D≌△DB'A
【答案】(1)见解析;(2)见解析.
【解析】
(1)先根据SAS证明△C′BD≌△ABC,得到C′D=AC= B′C,再利用SAS证明△BCA≌△DCB′,得到DB′=BA= BC′,最后根据SSS即可证明△C′BD≌△B′DC;
(2)由(1)可知,C′D=B′C=AB′,B′D=BC′=AC′,根据SSS即可证明△AC′D≌△DB′A.
证明:(1)∵∠DBC=60°,BC=DC,
∴△BCD为等边三角形,
∴BD=BC=CD,∠DBC=∠DCB=∠BDC=60°,
∵△ABC′为等边三角形,
∴BC′=AB=AC′,∠AB C′=60°,
∴∠DBC=∠ABC′,
∴∠DBC+∠ABD=∠ABC′+∠ABD,即∠ABC =∠C′BD,
在△ABC与△C′BD中,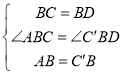 ,
,
∴△ABC≌△C′BD (SAS),
∴C′D=AC,
∵△AB′C为等边三角形,
∴AC= B′C=AB′,∠ACB′=∠AB′C=∠B′AC=60°,
∴C′D= B′C,
在△BCA与△DCB′中,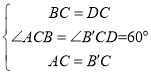 ,
,
∴△BCA≌△DCB′(SAS),
∴DB′=BA= BC′,
在△B′DC与△C′BD中,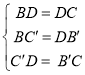 ,
,
∴△C′BD≌△B′DC(SSS);
(2)由(1)知:C′D=B′C=AB′,B′D=BC′=AC′,
又∵AD=AD,
∴在△AC′D与△DB′A中,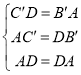 ,
,
∴△AC′D≌△DB′A(SSS).

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目