题目内容
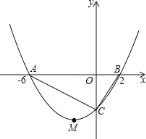
【题目】如图所示,抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点,且
两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求抛物线的函数解析式;
求抛物线的函数解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 能否在抛物线第三象限的图象上找到一点
能否在抛物线第三象限的图象上找到一点![]() ,使
,使![]() 的面积最大?若能,请求出点
的面积最大?若能,请求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标是
的坐标是![]() .
.
【解析】
(1)根据顶点坐标公式即可求得a、b、c的值,即可解题;
(2)易求得点B、C的坐标,即可求得OC的长,即可求得![]() 的面积,即可解题;
的面积,即可解题;
(3)作PE⊥x轴于点E,交AC于点F,可将![]() 的面积转化为
的面积转化为![]() 和
和![]() 的面积之和,而这两个三角形有共同的底PF,这一个底上的高的和又恰好是A、C两点间的距离,因此若设设E(x,0),则可用x来表示
的面积之和,而这两个三角形有共同的底PF,这一个底上的高的和又恰好是A、C两点间的距离,因此若设设E(x,0),则可用x来表示![]() 的面积,得到关于x的一个二次函数,求得该二次函数最大值,即可解题.
的面积,得到关于x的一个二次函数,求得该二次函数最大值,即可解题.
![]() 设此函数的解析式为
设此函数的解析式为![]() ,
,
∵函数图象顶点为![]() ,
,
∴![]() ,
,
又∵函数图象经过点![]() ,
,
∴![]()
解得![]() ,
,
∴此函数的解析式为![]() ,即
,即![]() ;
;
![]() ∵点
∵点![]() 是函数
是函数![]() 的图象与
的图象与![]() 轴的交点,
轴的交点,
∴点![]() 的坐标是
的坐标是![]() ,
,
又当![]() 时,有
时,有![]() ,
,
解得![]() ,
,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
则![]() ;
;
![]() 假设存在这样的点,过点
假设存在这样的点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() .
.
设![]() ,则
,则![]() ,
,

设直线![]() 的解析式为
的解析式为![]() ,
,
∵直线![]() 过点
过点![]() ,
,![]() ,
,
∴![]() ,
,
解得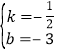 ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,
∴![]()
![]()
![]() ,
,
∴当![]() 时,
时,![]() 有最大值
有最大值![]() ,
,
此时点![]() 的坐标是
的坐标是![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目