题目内容
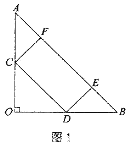
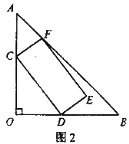
【题目】如图,两个直角∠AOC和∠BOD有公共顶点O,下列结论:
①∠AOB=∠COD;
②∠AOB+∠COD= ![]() ;
;
③若OB平分∠AOC,则OC平分∠BOD;
④∠AOD的平分线与∠BOC的平分线是同一条射线,
其中正确的是 . (填序号)
【答案】①③④.
【解析】因为∠AOC和∠BOD是两个直角,
所以∠AOB与∠COD都与∠BOC互余,
所以∠AOB=∠COD;
故①正确;也能得出②错误;
若OB平分∠AOC,则∠AOB=∠BOC=45,
从而得出∠COD=45,
故③正确;
此时∠AOD=135,设∠AOD的平分线为OE, 可算出∠BOE=∠COE=22.5,
设∠BOC的平分线为OF,则∠BOF=∠COF=22.5,
从而得出∠AOD的平分线与∠BOC的平分线是同一条射线,
故④正确;
综上所述,正确的序号是①③④.
抓住已知条件两个直角∠AOC和∠BOD有公共顶点O,根据同角的余角相等,可对①②作出判断;根据角平分线的定义,可对③④作出判断。从而得出答案。

【题目】有这样一个问题:探究函数y=![]() 的图象与性质。小慧根据学习函数的经验,对函数y=
的图象与性质。小慧根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究。下面是小慧的探究过程,请补充完成:
的图象与性质进行了探究。下面是小慧的探究过程,请补充完成:
(1)函数y=![]() 的自变量x的取值范围是__________;
的自变量x的取值范围是__________;
(2)列出y与x的几组对应值。请直接写出m的值,m=________;
x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出该函数的两条性质:
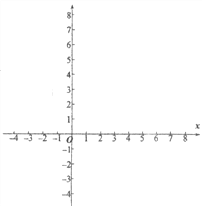
①_____________________________________________;
②____________________________________________。